الشافعية فقه - الفرائض ج 21
 والأصول التي
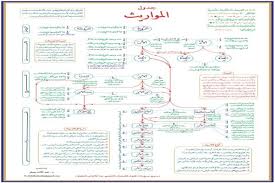
تعول هي: (6)، (12) (24).
والأصول التي
تعول هي: (6)، (12) (24).والثاني: لا يدخله عول أبداً.
والأصول التي لا تعول هي: (2)، (3)، (4)، (8).
ودليل عول تلك، وعدم عول هذه إنما هو استقراء المسائل، فبعد استقراء العلماء
لمسائل الفرائض تبين لهم ذلك، فحكموا به.
تعريف العول:
العول في اللغة، يأتي بمعنى الارتفاع، والزيادة، كما يأتي بمعنى الميل والجور، وتجاوز الحد، ومنه قول الله تبارك وتعالى: { ذَلِكَ أَدْنَى أَلاَّ تَعُولُواْ } [ النساء : 3]. أي أقرب إلى عدم الجور والظلم.
والعول اصطلاحاً: زيادة مجموع السهام عن أصل المسألة، ويلزم منه نقصان من مقادير أنصباء الورثة من التركة.
دليل مشروعية العول:
لم يقع العول في مسائل الفرائض في زمان النبي - صلى الله عليه وسلم -، ولا في زمان أبي بكر - رضي الله عنه -.
وأول من قال بالعول، ووقع في زمانه، عمر بن الخطاب - رضي الله عنه -.
فقد وقعت في عهده مسألة ضاق أصلها عن فروضها، فشاور - - رضي الله عنه - - الصحابة فيها، فأشار عليه زيد بن ثابت - رضي الله عنه - بالعول فوافق ذلك رأي عمر - رضي الله عنه -، وقال: ( والله ما أدري أيكم قدم الله، وأيكم أخر، وما أجد شيئاً هو أوسع لي أن أقسم المال عليكم بالحصص).
فأدخل على كل ذي حق ما دخل عليه من عول الفريضة، وقد وافقه الصحابة رضي الله عنهم، وبه أخذ جمهور العلماء، ومنهم الشافعي رحمه الله تعالى، وسيأتي كثير من صور المسائل التي فيها عول إن شاء الله تعالى.
الأصول التي تعول، ومدى عولها:
قلنا: إن أصول المسائل التي تعول هي: 6، 12، 24.
عول الستة:
تعول الستة، إلى (7، 8، 9، 10).
مثال عولها إلى سبعة:
7 عول
6
2/1 ... زوج ... 3
3/2 ... أختان شقيقتان ... 4
فالزوج له النصف، والشقيقتان لهما الثلثان، فأصل المسألة ستة، وتعول إلى سبعة.
ومثال عولها إلى ثمانية:
8 عول
6
2/1 ... زوج ... 3
3/2 ... شقيقتان ... 4
6/1 ... أم ... 1
للزوج النصف
ثلاثة، وللشقيقتين الثلثان أربعة، وللأم السدس واحد.
فأصل المسألة ستة، وقد عالت فروضها إلى ثمانية.
ومثال عولها إلى تسعة:
9 عول
6
2/1 ... زوج ... 3
3/2 ... أختان لأب ... 4
3/1 ... أختان لأم ... 2
للزوج النصف ثلاثة، وللأختين لأب الثلثان أربعة، وللأختين لأم الثلث اثنان، فأصل المسألة من ستة، وتعول إلى تسعة.
مثال عولها إلى عشرة:
10 عول
6
2/1 ... زوج ... 3
3/2 ... شقيقتان ... 4
3/1 ... أختان لأم ... 2
6/1 ... أم ... 1
للزوج النصف، وللشقيقتين الثلثان، وللأختين لأم الثلث، وللأم السدس، فأصل المسألة ستة، وتعول إلى عشرة.
عول الاثنى عشر:
ويعول الأصل الإثنا عشر إلى (13-15-17).
ومثال عولها إلى (13):
13 عول
12
4/1 ... زوجة ... 3
3/2 ... شقيقتان ... 8
6/1 ... أخت لأم ... 2
للزوجة الربع، وللشقيقتين الثلثان، وللأخت لأم السدس، أصل المسألة (12)، وتعول إلى (13).
مثال عولها إلى (15):
15 عول
12
4/1 ... زوجة ... 3
3/2 ... شقيقتان ... 8
3/1 ... أختان لأم ... 4
مثال عولها إلى (17):
17 عول
12
4/1 ... زوجة ... 3
3/2 ... شقيقتان ... 8
3/1 ... أخوان لأم ... 4
6/1 ... أم ... 2
للزوجة الربع (3)، وللشقيقتين الثلثان(8)، وللأخوين لأم الثلث (4)، وللأم السدس (2). وأصل المسألة (12)، وتعول إلى (17).
عول الأربعة والعشرين:
ويعول هذا الأصل إلى (27) فقط. مثال ذلك:
27 عول
24
8/1 ... زوجة ... 3
3/2 ... بنتان ... 16
6/1 ... أب ... 4
6/1 ... أم ... 4
للزوجة الثمن (3)، وللبنتين الثلثان (16)، وللأب السدس (4)، وللأم السدس (4)، فأصل المسألة (24)، وقد عالت إلى (27).
القاعدة في استخراج أصول المسائل:
الطريقة العملية لاستخراج أصول المسائل إنما تتم، وفق الترتيب التالي:
أن تكون المخارج في المسألة متماثلة، مثل (6/1 ، 6/1) كأب، وأم، وابن.
فيؤخذ أحد المتماثلات، ويجعل أصلاً للمسألة.
6
6/1 ... أب ... 1
6/1 ... أم ... 1
فأصل المسألة ستة، وقد عالت فروضها إلى ثمانية.
ومثال عولها إلى تسعة:
9 عول
6
2/1 ... زوج ... 3
3/2 ... أختان لأب ... 4
3/1 ... أختان لأم ... 2
للزوج النصف ثلاثة، وللأختين لأب الثلثان أربعة، وللأختين لأم الثلث اثنان، فأصل المسألة من ستة، وتعول إلى تسعة.
مثال عولها إلى عشرة:
10 عول
6
2/1 ... زوج ... 3
3/2 ... شقيقتان ... 4
3/1 ... أختان لأم ... 2
6/1 ... أم ... 1
للزوج النصف، وللشقيقتين الثلثان، وللأختين لأم الثلث، وللأم السدس، فأصل المسألة ستة، وتعول إلى عشرة.
عول الاثنى عشر:
ويعول الأصل الإثنا عشر إلى (13-15-17).
ومثال عولها إلى (13):
13 عول
12
4/1 ... زوجة ... 3
3/2 ... شقيقتان ... 8
6/1 ... أخت لأم ... 2
للزوجة الربع، وللشقيقتين الثلثان، وللأخت لأم السدس، أصل المسألة (12)، وتعول إلى (13).
مثال عولها إلى (15):
15 عول
12
4/1 ... زوجة ... 3
3/2 ... شقيقتان ... 8
3/1 ... أختان لأم ... 4
مثال عولها إلى (17):
17 عول
12
4/1 ... زوجة ... 3
3/2 ... شقيقتان ... 8
3/1 ... أخوان لأم ... 4
6/1 ... أم ... 2
للزوجة الربع (3)، وللشقيقتين الثلثان(8)، وللأخوين لأم الثلث (4)، وللأم السدس (2). وأصل المسألة (12)، وتعول إلى (17).
عول الأربعة والعشرين:
ويعول هذا الأصل إلى (27) فقط. مثال ذلك:
27 عول
24
8/1 ... زوجة ... 3
3/2 ... بنتان ... 16
6/1 ... أب ... 4
6/1 ... أم ... 4
للزوجة الثمن (3)، وللبنتين الثلثان (16)، وللأب السدس (4)، وللأم السدس (4)، فأصل المسألة (24)، وقد عالت إلى (27).
القاعدة في استخراج أصول المسائل:
الطريقة العملية لاستخراج أصول المسائل إنما تتم، وفق الترتيب التالي:
أن تكون المخارج في المسألة متماثلة، مثل (6/1 ، 6/1) كأب، وأم، وابن.
فيؤخذ أحد المتماثلات، ويجعل أصلاً للمسألة.
6
6/1 ... أب ... 1
6/1 ... أم ... 1
ع ... ابن ...
4
2- أن تكون المخارج في المسألة متداخلة، وذلك، بأن يكون بعضها أكبر من بعض، ويكون الأكبر منها ينقسم على الأصغر، مثل (3/1-2/1-6/1)، فإن الثلاثة، والاثنين، تدخلان في الستة.
وكذلك مثل (2/1 -8/1)، فإن الاثنين تدخل في الثمانية.
8
8/1 ... زوجة ... 1
2/1 ... بنت ... 4
ع ... عم ... 3
ففي حالة التداخل، يؤخذ المخرج الأكبر، ويجعل أصلاً للمسألة:
6
3/1 ... أخوان لأم ... 2
2/1 ... أخت لأب ... 3
6/1 ... أم ... 1
3- أن تكون المخارج في المسألة متوافقة، وذلك بأن تكون تقبل القسمة على عدد معين مثل:8/1 ،6/1، بينهما توافق بالنصف، لأن كلاً منهما يقبل القسمة على اثنين.
ففي حالة التوافق يؤخذ وفق أحد المخرجين، وهو نصفه مثلاً في المثال السابق، ويضرب بكامل المخرج الآخر، ويكون الحاصل هو أصل المسألة، ففي مثالنا السابق يضرب نصف الثمانية بكامل الستة، أو نصف الستة بكامل الثمانية، والحاصل وهو: (24) يكون أثل المسألة، وصورة ذلك:
24
6/1 ... أم ... 4
8/1 ... زوجة ... 3
2/1 ... بنت ... 12
ع ... عم ... 5
فالمخرج اثنان يدخل في كل من الستة، والثمانية، فنتركه، ونأخذ الأكبر منه.
والمخرج ستة وثمانية ليسا متداخلين، بل هما متوافقان، بالنصف، فيؤخذ نصف أحدهما ويضرب به كامل الآخر، فيكون الناتج هو أصل المسألة، كما هو موضح في صورة المسألة السابقة.
4- أن تكون المخارج متباينة، وذلك بأن تكون غير متماثلة، ولا متداخلة، ولا متوافقة، مثل (4/1-3/1)، فبين المخرجين 3-4 تباين، لأنهما غير متماثلين، ولا يقبل أحدهما القسمة على الآخر، ولا يقبلان القسمة على عدد واحد.
ففي هذه الحالة يضرب كامل أحدهما بكامل الآخر، ويكون الحاصل هو أصل المسألة. وصورة هذا:
12
4/1 ... زوجة ... 3
3/1 ... أم ... 4
ع ... عم ... 5
2- أن تكون المخارج في المسألة متداخلة، وذلك، بأن يكون بعضها أكبر من بعض، ويكون الأكبر منها ينقسم على الأصغر، مثل (3/1-2/1-6/1)، فإن الثلاثة، والاثنين، تدخلان في الستة.
وكذلك مثل (2/1 -8/1)، فإن الاثنين تدخل في الثمانية.
8
8/1 ... زوجة ... 1
2/1 ... بنت ... 4
ع ... عم ... 3
ففي حالة التداخل، يؤخذ المخرج الأكبر، ويجعل أصلاً للمسألة:
6
3/1 ... أخوان لأم ... 2
2/1 ... أخت لأب ... 3
6/1 ... أم ... 1
3- أن تكون المخارج في المسألة متوافقة، وذلك بأن تكون تقبل القسمة على عدد معين مثل:8/1 ،6/1، بينهما توافق بالنصف، لأن كلاً منهما يقبل القسمة على اثنين.
ففي حالة التوافق يؤخذ وفق أحد المخرجين، وهو نصفه مثلاً في المثال السابق، ويضرب بكامل المخرج الآخر، ويكون الحاصل هو أصل المسألة، ففي مثالنا السابق يضرب نصف الثمانية بكامل الستة، أو نصف الستة بكامل الثمانية، والحاصل وهو: (24) يكون أثل المسألة، وصورة ذلك:
24
6/1 ... أم ... 4
8/1 ... زوجة ... 3
2/1 ... بنت ... 12
ع ... عم ... 5
فالمخرج اثنان يدخل في كل من الستة، والثمانية، فنتركه، ونأخذ الأكبر منه.
والمخرج ستة وثمانية ليسا متداخلين، بل هما متوافقان، بالنصف، فيؤخذ نصف أحدهما ويضرب به كامل الآخر، فيكون الناتج هو أصل المسألة، كما هو موضح في صورة المسألة السابقة.
4- أن تكون المخارج متباينة، وذلك بأن تكون غير متماثلة، ولا متداخلة، ولا متوافقة، مثل (4/1-3/1)، فبين المخرجين 3-4 تباين، لأنهما غير متماثلين، ولا يقبل أحدهما القسمة على الآخر، ولا يقبلان القسمة على عدد واحد.
ففي هذه الحالة يضرب كامل أحدهما بكامل الآخر، ويكون الحاصل هو أصل المسألة. وصورة هذا:
12
4/1 ... زوجة ... 3
3/1 ... أم ... 4
ع ... عم ... 5
فبين الربع
نصيب الزوجة، وبين الثل نصيب الأم تباين، فيضرب أحدهما بالآخر، ويكون الحاصل أصل
المسألة، كما هو مبين في صورة المسألة السابقة.
تصحيح المسائل، وطريقة ذلك:
قلنا فيما سبق: إن تصحيح المسألة: هو أقل عدد يتأتى منه نصيب كل واحد من الورثة صحيحاً دون كسر.
وهنا نقول: إذا كانت المسألة تصح من أصلها، وذلك بأن كان نصيب كل فريق من الورثة منقسماً على عدد رؤوسهم، فإنه والحالة هذه، يقتصر في القسمة على أصل المسألة، ولا تحتاج إلى تصحيح، بل يعطى كل وارث سهمه كاملاً من أصل المسألة، إن لم تكن المسألة عائلة، أ, يعطي نصيبه من عولها، إذا كانت عائلة.
فلو كان لدينا مثلاً مسألة فيها:
12
4/1 ... ثلاث زوجات ... 3
3/1 ... أم ... 4
ع ... خمسة أعمام ... 5
فأصل هذه المسألة (12)، وذلك بضرب مخرج الربع بمخرج الثلث، لأنهما متباينان، فيضرب ثلاثة في أربعة، فيتحصل اثنا عشر، هو أصل المسألة، وهذه المسألة، تصح من أصلها، إذ ينقسم نصيب كل فريق من الورثة على عدد رؤوسهم من غير كسر.
فتأخذ الزوجات الربع ثلاثة أسهم، وهي منقسمة عليهم، إذ لكل زوجة سهم.
وتأخذ الأم الثلث، أربعة أسهم.
ويأخذ الأعمام الباقي تعصيباً، وهو خمسة أسهم، وهي منقسمة عليهم، إذ يأخذ كل عم سهماً واحداً.
وهكذا كل مسألة تصح من أصلها، لا تحتاج إلى تصحيح، لأن التصحيح عندئذ تطويل من غير فائدة. وكذلك إذا عالت المسألة، وانقسم عولها على الورثة، فإنها لا تحتاج إلى تصحيح أيضاً. وصورة ذلك:
17 عول
12
6/1 ... جدتان ... 2
4/1 ... ثلاث زوجات ... 3
3/1 ... أربع أخوات لأم ... 4
3/2 ... ثمان أخوات لأب ... 8
فهذه المسألة أصلها من (12) أخذاً من ضرب نصف مخرج الربع، وهو اثنان، بكامل مخرج السدس، وهو ستة، لأن بين المخرجين توافقاً في النصف، وتعول المسألة إلى سبعة عشر.
فتأخذ الجدتان السدس عائلاً، وهو سهمان من سبعة عشر سهماً، لكل جدة سهم.
تصحيح المسائل، وطريقة ذلك:
قلنا فيما سبق: إن تصحيح المسألة: هو أقل عدد يتأتى منه نصيب كل واحد من الورثة صحيحاً دون كسر.
وهنا نقول: إذا كانت المسألة تصح من أصلها، وذلك بأن كان نصيب كل فريق من الورثة منقسماً على عدد رؤوسهم، فإنه والحالة هذه، يقتصر في القسمة على أصل المسألة، ولا تحتاج إلى تصحيح، بل يعطى كل وارث سهمه كاملاً من أصل المسألة، إن لم تكن المسألة عائلة، أ, يعطي نصيبه من عولها، إذا كانت عائلة.
فلو كان لدينا مثلاً مسألة فيها:
12
4/1 ... ثلاث زوجات ... 3
3/1 ... أم ... 4
ع ... خمسة أعمام ... 5
فأصل هذه المسألة (12)، وذلك بضرب مخرج الربع بمخرج الثلث، لأنهما متباينان، فيضرب ثلاثة في أربعة، فيتحصل اثنا عشر، هو أصل المسألة، وهذه المسألة، تصح من أصلها، إذ ينقسم نصيب كل فريق من الورثة على عدد رؤوسهم من غير كسر.
فتأخذ الزوجات الربع ثلاثة أسهم، وهي منقسمة عليهم، إذ لكل زوجة سهم.
وتأخذ الأم الثلث، أربعة أسهم.
ويأخذ الأعمام الباقي تعصيباً، وهو خمسة أسهم، وهي منقسمة عليهم، إذ يأخذ كل عم سهماً واحداً.
وهكذا كل مسألة تصح من أصلها، لا تحتاج إلى تصحيح، لأن التصحيح عندئذ تطويل من غير فائدة. وكذلك إذا عالت المسألة، وانقسم عولها على الورثة، فإنها لا تحتاج إلى تصحيح أيضاً. وصورة ذلك:
17 عول
12
6/1 ... جدتان ... 2
4/1 ... ثلاث زوجات ... 3
3/1 ... أربع أخوات لأم ... 4
3/2 ... ثمان أخوات لأب ... 8
فهذه المسألة أصلها من (12) أخذاً من ضرب نصف مخرج الربع، وهو اثنان، بكامل مخرج السدس، وهو ستة، لأن بين المخرجين توافقاً في النصف، وتعول المسألة إلى سبعة عشر.
فتأخذ الجدتان السدس عائلاً، وهو سهمان من سبعة عشر سهماً، لكل جدة سهم.
وتأخذ الزوجات
الربع عائلاً، وهو ثلاثة أسهم من سبعة عشر سهماً، لكل زوجة سهم.
وتأخذ الأخوات لأم الثلث عائلاً، وهو أربعة أسهم من سبعة عشر سهماً، لكل أخت سهم.
وتأخذ الأخوات لأب الثلثين عائلاً، وهو ثمانية أسهم من سبعة عشر سهماً، لكل واحدة منهن سهم. وتعرف هذه المسألة في الفرائض: ( بأم الأرامل).
أما إذا كانت سهام كل فريق من أصل المسألة، أو من عولها، لا تنقسم على عدد رؤوسهم قسمة صحيحة من غير كسر، فإن المسألة – والحالة هذه – يجب تصحيحها، وذلك برفع أصلها إلى أقل عدد يتأتى منه نصيب كل فريق من الورثة صحيحاً من غير كسر.
وتصحيح المسألة إنما يتم وفق الترتيب التالي:
أن يكون الانكسار في المسألة على فريق واحد من الورثة، مثال ذلك:
(جزء السهم)
3× ... (أصل)
6 ... (تصحيح)
18
6/1 ... أم ... 1 ... 3
6/1 ... أب ... 1 ... 3
ع ... ثلاثة أبناء ... 4 ... 12
فإن المسألة من ستة، لتماثل مخرجيها، للأب السدس واحد، وللأم السدس واحد، والباقي للأبناء، وهو أربعة أسهم وهي غير منقسمة على ثلاثة أبناء قسمة صحيحة من غير كسر، وعندئذ نحتاج إلى تصحيح المسألة، وذلك بأن ننظر بين سهام هذا الفريق، وعدد رؤوسهم. فإما أن يكون بين عدد الرؤوس والسهام تباين، أو توافق. ولا اعتبار هنا للتداخل، والتماثل، لأن السهام عندئذ تكن منقسمة.
فإذا كان بين عدد الرؤوس والسهام تباين، فإننا نضرب أصل المسألة بعدد الرؤوس، وحاصل الضرب يكون هو تصحيح المسألة، كما في المسألة السابقة، ضربنا أصل المسألة (6) بعدد رؤوس الأبناء الثلاثة (6×3=18) = هو تصحيح المسألة.
ويسمى عدد الرؤوس جزء السهم.
ثم نضرب بجزء السهم هذا نصيب كل فريق من الورثة، ومنه ينقسم نصيب ذلك الفريق على عدد رؤوسه.
وتأخذ الأخوات لأم الثلث عائلاً، وهو أربعة أسهم من سبعة عشر سهماً، لكل أخت سهم.
وتأخذ الأخوات لأب الثلثين عائلاً، وهو ثمانية أسهم من سبعة عشر سهماً، لكل واحدة منهن سهم. وتعرف هذه المسألة في الفرائض: ( بأم الأرامل).
أما إذا كانت سهام كل فريق من أصل المسألة، أو من عولها، لا تنقسم على عدد رؤوسهم قسمة صحيحة من غير كسر، فإن المسألة – والحالة هذه – يجب تصحيحها، وذلك برفع أصلها إلى أقل عدد يتأتى منه نصيب كل فريق من الورثة صحيحاً من غير كسر.
وتصحيح المسألة إنما يتم وفق الترتيب التالي:
أن يكون الانكسار في المسألة على فريق واحد من الورثة، مثال ذلك:
(جزء السهم)
3× ... (أصل)
6 ... (تصحيح)
18
6/1 ... أم ... 1 ... 3
6/1 ... أب ... 1 ... 3
ع ... ثلاثة أبناء ... 4 ... 12
فإن المسألة من ستة، لتماثل مخرجيها، للأب السدس واحد، وللأم السدس واحد، والباقي للأبناء، وهو أربعة أسهم وهي غير منقسمة على ثلاثة أبناء قسمة صحيحة من غير كسر، وعندئذ نحتاج إلى تصحيح المسألة، وذلك بأن ننظر بين سهام هذا الفريق، وعدد رؤوسهم. فإما أن يكون بين عدد الرؤوس والسهام تباين، أو توافق. ولا اعتبار هنا للتداخل، والتماثل، لأن السهام عندئذ تكن منقسمة.
فإذا كان بين عدد الرؤوس والسهام تباين، فإننا نضرب أصل المسألة بعدد الرؤوس، وحاصل الضرب يكون هو تصحيح المسألة، كما في المسألة السابقة، ضربنا أصل المسألة (6) بعدد رؤوس الأبناء الثلاثة (6×3=18) = هو تصحيح المسألة.
ويسمى عدد الرؤوس جزء السهم.
ثم نضرب بجزء السهم هذا نصيب كل فريق من الورثة، ومنه ينقسم نصيب ذلك الفريق على عدد رؤوسه.
فلما كان نصيب
الأبناء الثلاثة في المسألة (4) وهي غير منقسمة عليهم، فإننا نضربها بجزء السهم،
وهو ثلاثة عدد الرؤوس، وحاصل الضرب، يساوي (12) وهي منقسمة عليهم، إذ يكون نصيب كل
ابن (4) أسهم.
أما إذا كان بين عدد الرؤوس، وبين السهام توافق فإننا نأخذ وفق الرؤوس، ونضرب به أصل المسألة، فمنه تصح المسألة.
ثم نضرب بذلك الوفق نصيب كل فريق من الورثة، فينقسم على عدد رؤوسهم.
ومثال ذلك:
(جزء السهم)
2× ... (أصل)
6 ... (تصحيح)
12
2/1 ... زوج ... 3 ... 6
6/1 ... جدة ... 1 ... 2
ع ... أربعة أعمام ... 2 ... 4
ففي هذا المثال كان أصل المسألة (6) لأن بين مخرجي النصف والسدس تداخلاً، فنأخذ المخرج الأكبر وهو (6) ونجعله أصل المسألة.
ونصيب الزوج (3) أسهم من ستة، وهي النصف، ونصيب الجدة السدس، وهو سهم واحد، ونصيب الأعمام السهمان الباقيان، تعصيباً، وهما غير منقسمين على رؤوس الأعمام الأربعة، لذلك صححنا المسألة، بضربها بوفق رؤوس الأعمام (2)؛ إذ بين الرؤوس وبين السهام توافق ضربنا بجزء السهم، وهو وفق الرؤوس، نصيب كل فريق من الورثة، فانقسمت بذلك السهام على عدد الرؤوس.
2- أن يكون الانكسار في المسألة على أكثر من فريق أي على فريقين من الورثة، أو ثلاثة، أو أربعة، ولا يكون الانكسار في مسائل الفرائض على أكثر من ذلك.
وهنا من أجل تصحيح المسألة، لابد من النظر بين رؤوس كل فريق، وسهامه. ثم نحفظ رؤوس كل فريق عند المباينة، أو وفقها عند الموافقة.
ثم بعد هذا ننظر بين هذه المحفوظات بالنسب الأربع: التماثل، والتداخل، والتوافق، والتباين، فإن تماثلت أخذنا مثلاً واحداً، وضربنا به أصل المسألة وإن تداخلت أخذنا الأكبر منها، وضربنا به أصل المسألة.
وإن توافقت، أخذنا الوفق وضربنا به كامل العدد الآخر، وضربنا بالحاصل أصل المسألة.
وإذا تباينت ضربنا الرؤوس بعضها ببعض، ثم ضربنا بالحاصل أصل المسألة، ومنه تصح تلك المسألة.
أما إذا كان بين عدد الرؤوس، وبين السهام توافق فإننا نأخذ وفق الرؤوس، ونضرب به أصل المسألة، فمنه تصح المسألة.
ثم نضرب بذلك الوفق نصيب كل فريق من الورثة، فينقسم على عدد رؤوسهم.
ومثال ذلك:
(جزء السهم)
2× ... (أصل)
6 ... (تصحيح)
12
2/1 ... زوج ... 3 ... 6
6/1 ... جدة ... 1 ... 2
ع ... أربعة أعمام ... 2 ... 4
ففي هذا المثال كان أصل المسألة (6) لأن بين مخرجي النصف والسدس تداخلاً، فنأخذ المخرج الأكبر وهو (6) ونجعله أصل المسألة.
ونصيب الزوج (3) أسهم من ستة، وهي النصف، ونصيب الجدة السدس، وهو سهم واحد، ونصيب الأعمام السهمان الباقيان، تعصيباً، وهما غير منقسمين على رؤوس الأعمام الأربعة، لذلك صححنا المسألة، بضربها بوفق رؤوس الأعمام (2)؛ إذ بين الرؤوس وبين السهام توافق ضربنا بجزء السهم، وهو وفق الرؤوس، نصيب كل فريق من الورثة، فانقسمت بذلك السهام على عدد الرؤوس.
2- أن يكون الانكسار في المسألة على أكثر من فريق أي على فريقين من الورثة، أو ثلاثة، أو أربعة، ولا يكون الانكسار في مسائل الفرائض على أكثر من ذلك.
وهنا من أجل تصحيح المسألة، لابد من النظر بين رؤوس كل فريق، وسهامه. ثم نحفظ رؤوس كل فريق عند المباينة، أو وفقها عند الموافقة.
ثم بعد هذا ننظر بين هذه المحفوظات بالنسب الأربع: التماثل، والتداخل، والتوافق، والتباين، فإن تماثلت أخذنا مثلاً واحداً، وضربنا به أصل المسألة وإن تداخلت أخذنا الأكبر منها، وضربنا به أصل المسألة.
وإن توافقت، أخذنا الوفق وضربنا به كامل العدد الآخر، وضربنا بالحاصل أصل المسألة.
وإذا تباينت ضربنا الرؤوس بعضها ببعض، ثم ضربنا بالحاصل أصل المسألة، ومنه تصح تلك المسألة.
ونذكر لهذه
الصور أمثلة توضحها:
المثال الأول: تماثل عدد الرؤوس:
(جزء السهم)
5× ... (أصل)
6 ... (تصحيح)
30
6/1 ... أم ... 1 ... 5
3/1 ... خمسة أخوة لأم ... 2 ... 10
ع ... خمسة أعمام ... 3 ... 15
ففي هذه المسألة، كان الانكسار على فريقين: الإخوة لأم، والأعمام.
أصل المسألة من ستة، وذلك لتداخل مخرجيها (3/1 – 6/1).نصيب الأم السدس (1)، ونصيب الإخوة لأم الثلث (2) وهو غير منقسم عليهم، ونصيب الأعمام الباقي تعصيباً(3) وهو أيضاً غير منقسم عليهم.
وبعد هذا ننظر بين سهام الإخوة لأم، وبين عدد رؤوسهم، وظاهر أن بينهما تبايناً. فنأخذ عدد الرؤوس، وهي خمسة، ونحفظها.
ثم ننظر أيضاً بين عدد رؤوس الأعمام وبين سهامهم، وبينهما أيضاً تباين، فنحفظ عدد الرؤوس.
ثم ننظر بين عدد الرؤوس المحفوظة، وبينها كما هو واضح تماثل، إذ الأخوة لأم خمسة، والأعمام خمسة أيضاً.
فنأخذ مثلاً واحداً، ونضرب به أصل المسألة (12)، فيكون الحاصل (30) وهو تصحيح المسألة.
ثم نضرب بذلك المثل، وهو عدد الرؤوس، وهو ما نسميه جزء السهم – كما قلنا من قبل – نصيب كل فريق من الورثة، وبذلك تنقسم سهام كل فريق على عدد رؤوسهم، كما هو موضح في صورة المسألة السابقة.
المثال الثاني : تداخل عدد الرؤوس:
(جزء السهم)
4× ... (أصل)
6 ... (تصحيح)
24
6/1 ... أم ... 1 ... 4
3/1 ... أربعة أخوة لأم ... 2 ... 8
ع ... أربعة أعمام ... 3 ... 12
أصل هذه المسألة (6) لتداخل مخرجيها : (6/1 -3/1).
ونصيب الأم منها السدس (1)، ونصيب الإخوة لأم الثلث، وهو سهمان، وهما غير منقسمين عليهم، لكن بين السهام وعدد الرؤوس توافق بالنصف، فنأخذ وفق الرؤوس (2) ونحفظها. ونصيب الأعمام الباقي، تعصيباً، وهو (3) أسهم وهي غير منقسمة على الأعمام الأربعة، وبينهما تباين فنحفظ عدد الرؤوس، وهي أربعة.
المثال الأول: تماثل عدد الرؤوس:
(جزء السهم)
5× ... (أصل)
6 ... (تصحيح)
30
6/1 ... أم ... 1 ... 5
3/1 ... خمسة أخوة لأم ... 2 ... 10
ع ... خمسة أعمام ... 3 ... 15
ففي هذه المسألة، كان الانكسار على فريقين: الإخوة لأم، والأعمام.
أصل المسألة من ستة، وذلك لتداخل مخرجيها (3/1 – 6/1).نصيب الأم السدس (1)، ونصيب الإخوة لأم الثلث (2) وهو غير منقسم عليهم، ونصيب الأعمام الباقي تعصيباً(3) وهو أيضاً غير منقسم عليهم.
وبعد هذا ننظر بين سهام الإخوة لأم، وبين عدد رؤوسهم، وظاهر أن بينهما تبايناً. فنأخذ عدد الرؤوس، وهي خمسة، ونحفظها.
ثم ننظر أيضاً بين عدد رؤوس الأعمام وبين سهامهم، وبينهما أيضاً تباين، فنحفظ عدد الرؤوس.
ثم ننظر بين عدد الرؤوس المحفوظة، وبينها كما هو واضح تماثل، إذ الأخوة لأم خمسة، والأعمام خمسة أيضاً.
فنأخذ مثلاً واحداً، ونضرب به أصل المسألة (12)، فيكون الحاصل (30) وهو تصحيح المسألة.
ثم نضرب بذلك المثل، وهو عدد الرؤوس، وهو ما نسميه جزء السهم – كما قلنا من قبل – نصيب كل فريق من الورثة، وبذلك تنقسم سهام كل فريق على عدد رؤوسهم، كما هو موضح في صورة المسألة السابقة.
المثال الثاني : تداخل عدد الرؤوس:
(جزء السهم)
4× ... (أصل)
6 ... (تصحيح)
24
6/1 ... أم ... 1 ... 4
3/1 ... أربعة أخوة لأم ... 2 ... 8
ع ... أربعة أعمام ... 3 ... 12
أصل هذه المسألة (6) لتداخل مخرجيها : (6/1 -3/1).
ونصيب الأم منها السدس (1)، ونصيب الإخوة لأم الثلث، وهو سهمان، وهما غير منقسمين عليهم، لكن بين السهام وعدد الرؤوس توافق بالنصف، فنأخذ وفق الرؤوس (2) ونحفظها. ونصيب الأعمام الباقي، تعصيباً، وهو (3) أسهم وهي غير منقسمة على الأعمام الأربعة، وبينهما تباين فنحفظ عدد الرؤوس، وهي أربعة.
ثم ننظر بين
رؤوس الأعمام (4)، وبين وفق رؤوس الإخوة لأم (2)، فنجد بينهما تداخلاً، إذ العدد
(2) يدخل في العدد (4).
فنأخذ العدد الأكبر، وهو (4) ونضرب به أصل المسألة السابقة (6)، فيكون الناتج (24) وهو تصحيح المسألة. ثم نضرب بجزء السهم، وهو الأربعة، عدد رؤوس الأعمام، سهام كل فرق، فيكون الناتج منقسماً على عدد رؤوس كل فريق.
كما هو موضح في صورة المسألة السابقة.
المثال الثالث: توافق الرؤوس:
(جزء السهم)
30× ... (أصل)
6 ... (تصحيح)
180
6/1 ... أم ... 1 ... 30
3/1 ... 15 أخ لأم ... 2 ... 60
ع ... 10 أعمام ... 3 ... 90
أصل هذه المسألة (6). نصيب الأم سهم واحد، ونصيب الإخوة لأم سهمان، وهي غير منقسمة على عدد رؤوس الإخوة الخمسة عشر، وبين السهام وعد الرؤوس تباين، فنحفظ عدد الرؤوس (15)، ونصيب الأعمام الباقي، تعصيباً وهي ثلاثة أسهم، وهي غير منقسمة على الأعمام العشرة، وبين السهام وبين عدد الرؤوس تباين أيضاً، فنحفظ عدد الرؤوس (10).
ثم ننظر بين رؤوس الإخوة لأم الخمسة وبين رؤوس الأعمام العشرة، فنجد بينها توافقاً في الخمس، فنأخذ وفق رؤوس أحدهما، ونضرب به كامل عدد الرؤوس الآخر، والحاصل نضرب به أصل المسألة فما بلغ فهو تصحيح المسألة:
أي نضرب أصل المسألة (6) بحاصل ضرب (2×15=30)، والبالغ (180) هو تصحيح المسألة. ثم نضرب بجزء السهم (30) نصيب كل وارث، فيكون الحاصل لكل فريق، منقسماً على عدد رؤوسهم، وهذا موضح في صورة المسألة السابقة.
المثال الرابع : تباين الرؤوس:
(جزء السهم)
6× ... (أصل)
6 ... (تصحيح)
36
6/1 ... أم ... 1 ... 6
3/1 ... 3 أخوة لأم ... 2 ... 12
ع ... 2 عمان ... 3 ... 18
أصل المسألة ستة.
فنأخذ العدد الأكبر، وهو (4) ونضرب به أصل المسألة السابقة (6)، فيكون الناتج (24) وهو تصحيح المسألة. ثم نضرب بجزء السهم، وهو الأربعة، عدد رؤوس الأعمام، سهام كل فرق، فيكون الناتج منقسماً على عدد رؤوس كل فريق.
كما هو موضح في صورة المسألة السابقة.
المثال الثالث: توافق الرؤوس:
(جزء السهم)
30× ... (أصل)
6 ... (تصحيح)
180
6/1 ... أم ... 1 ... 30
3/1 ... 15 أخ لأم ... 2 ... 60
ع ... 10 أعمام ... 3 ... 90
أصل هذه المسألة (6). نصيب الأم سهم واحد، ونصيب الإخوة لأم سهمان، وهي غير منقسمة على عدد رؤوس الإخوة الخمسة عشر، وبين السهام وعد الرؤوس تباين، فنحفظ عدد الرؤوس (15)، ونصيب الأعمام الباقي، تعصيباً وهي ثلاثة أسهم، وهي غير منقسمة على الأعمام العشرة، وبين السهام وبين عدد الرؤوس تباين أيضاً، فنحفظ عدد الرؤوس (10).
ثم ننظر بين رؤوس الإخوة لأم الخمسة وبين رؤوس الأعمام العشرة، فنجد بينها توافقاً في الخمس، فنأخذ وفق رؤوس أحدهما، ونضرب به كامل عدد الرؤوس الآخر، والحاصل نضرب به أصل المسألة فما بلغ فهو تصحيح المسألة:
أي نضرب أصل المسألة (6) بحاصل ضرب (2×15=30)، والبالغ (180) هو تصحيح المسألة. ثم نضرب بجزء السهم (30) نصيب كل وارث، فيكون الحاصل لكل فريق، منقسماً على عدد رؤوسهم، وهذا موضح في صورة المسألة السابقة.
المثال الرابع : تباين الرؤوس:
(جزء السهم)
6× ... (أصل)
6 ... (تصحيح)
36
6/1 ... أم ... 1 ... 6
3/1 ... 3 أخوة لأم ... 2 ... 12
ع ... 2 عمان ... 3 ... 18
أصل المسألة ستة.
نصيب الأم سهم
واحد، ونصيب الإخوة لأم سهمان، وهما غير منقسمين على الإخوة لأم الثلاثة، وبين
الرؤوس والسهام تباين، فنحفظ عدد الرؤوس (3)، ونصيب العمين، ثلاثة أسهم، وهي غير
منقسمة على العمين، وبين الرؤوس والسهام تباين، فنحفظ عدد الرؤوس (2)، ثم ننظر بين
الرؤوس (2 ، 3) فنجد بينها تبايناً فنضرب كامل بعضها بكامل البعض الآخر (2×3=6)،
وحاصل الضرب، وهو (6)، يكون جزء السهم، نضرب به أصل المسألة (6×6=36)، وهذا هو
تصحيح المسألة.
ثم نضرب بجزء السهم (6) نصيب كل فريق من الورثة ويكون حاصل ضرب سهام كل فريق منقسماً على عدد رؤوسهم، كما هو مبين في المسألة السابقة.
قال الإمام الرحبي في (باب الحساب):
وإن ترد معرفة الحساب ... ... ... ... لتهتدي فيه إلى الصواب
وتعرف القسمة والتفصيلا ... ... ... ... وتعلم التصحيح والتأصيلا
فاستخرج الأصول في المسائل ... ... ... ولا تكن عن حفظها بذاهل(1)
فإنهن سبعة أصول ... ... ... ... ... ثلاثة منهن قد تعول
وبعدها أربعة تمام ... ... ... ... ... لا عول يعروها ولا انثلام(2)
فالسدس من ستة أسهم يرى ... ... ... ... والسدس والربع من اثنى عشرا
والثمن إن ضم إليه السدس ... ... ... ... فأصله الصادق فيه الحدس(3)
أربعة يتبعها عشرونا ... ... ... ... ... يعرفها الحساب أجمعونا
فهذه الثلاثة الأصول ... ... ... ... ... إن كثرت فروضها تعول
فتبلغ الستة عقد العشرة ... ... ... ... في صورة معروفة مشتهره وتلحق التي تليها في الأثر ... ... ... ... بالعول إفراداً إلى سبع عشر
والعدد الثالث قد يعول ... ... ... ... بثمنه فاعمل بما أقول
والنصف والباقي أو النصفان ... ... ... أصلهما في حكمهم إثنان
والثلث من ثلاثة يكون ... ... ... ... والربع من أربعة مسنون
__________
(1) بذاهل: متشاغل: تقول: ذهلت عن الشيء: تناسيته، وشغلت عنه.
(2) يعروها : يغشاها وينزل بها. ولا انثلام: كسر وخلل.
(3) الحدس: الظن والتخمين.
ثم نضرب بجزء السهم (6) نصيب كل فريق من الورثة ويكون حاصل ضرب سهام كل فريق منقسماً على عدد رؤوسهم، كما هو مبين في المسألة السابقة.
قال الإمام الرحبي في (باب الحساب):
وإن ترد معرفة الحساب ... ... ... ... لتهتدي فيه إلى الصواب
وتعرف القسمة والتفصيلا ... ... ... ... وتعلم التصحيح والتأصيلا
فاستخرج الأصول في المسائل ... ... ... ولا تكن عن حفظها بذاهل(1)
فإنهن سبعة أصول ... ... ... ... ... ثلاثة منهن قد تعول
وبعدها أربعة تمام ... ... ... ... ... لا عول يعروها ولا انثلام(2)
فالسدس من ستة أسهم يرى ... ... ... ... والسدس والربع من اثنى عشرا
والثمن إن ضم إليه السدس ... ... ... ... فأصله الصادق فيه الحدس(3)
أربعة يتبعها عشرونا ... ... ... ... ... يعرفها الحساب أجمعونا
فهذه الثلاثة الأصول ... ... ... ... ... إن كثرت فروضها تعول
فتبلغ الستة عقد العشرة ... ... ... ... في صورة معروفة مشتهره وتلحق التي تليها في الأثر ... ... ... ... بالعول إفراداً إلى سبع عشر
والعدد الثالث قد يعول ... ... ... ... بثمنه فاعمل بما أقول
والنصف والباقي أو النصفان ... ... ... أصلهما في حكمهم إثنان
والثلث من ثلاثة يكون ... ... ... ... والربع من أربعة مسنون
__________
(1) بذاهل: متشاغل: تقول: ذهلت عن الشيء: تناسيته، وشغلت عنه.
(2) يعروها : يغشاها وينزل بها. ولا انثلام: كسر وخلل.
(3) الحدس: الظن والتخمين.
والثمن إن كان
فمن ثمانية ... ... ... ... فهذه هي الأصول الثانيه
لا يدخل العول عليها فاعلم ... ... ... ... ثم اسلك التصحيح فيها تسلم
وإن تكن من أصلها تصح ... ... ... ... فترك تطويل الحساب ربح
فأعط كلاً سهمه من أصلها ... ... ... ... مكملاً أو عائلاً من عولها
وإن تر السهام ليست تنقسم ... ... ... ... على ذوي الميراث فاتبع ما رسم
واطلب طريق الاختصار في العمل ... ... بالوفق والضرب يجانبك الزلل(1)
واردد إلى الوفق الذي يوافق ... ... ... واضربه في الأصل فأنت الحاذق(2)
إن كان جنساً واحداً فأكثرا ... ... ... فاحفظ ودع عنك الجدال والمرا(3)
وإن تر الكسر على أجناس ... ... ... ... فإنها في الحكم عند الناس
تحصر في أربعة أقسام ... ... ... ... يعرفها الماهر في الأحكام(4)
مماثل من بعده مناسب ... ... ... ... وبعده موافق مصاحب
والرابع المباين المخالف ... ... ... ... ينبيك عن تفصيلهن العارف
فخذ من المماثلين واحداً ... ... ... ... وخذ من المناسبين الزائدا
واضرب جميع الوفق بالموافق ... ... ... واسلك بذاك أنهج الطرائق(5)
وخذ جميع العدد المباين ... ... ... ... واضربه في الثاني ولا تداهن(6)
فذاك جزء السهم فاعلمنه ... ... ... ... واحذر هديت أن تضل عنه
واضربه في الأصل الذي تأصلا ... ... ... وأحص ما انضم وما تحصلاً(7)
واقسمه فالقسم إذاً صحيح ... ... ... ... يعرفه الأعجم والفصيح(8)
فهذه من الحساب جمل ... ... ... ... يأتي على مثالهن العمل(9)
__________
(1) الزلل : الخطأ.
(2) الحاذق : العارف.
(3) المرا : الجدال والمخاصمة.
(4) الماهر : الحاذق
(5) أنهج الطرائق: أوضح الطرق.
(6) لا تداهن: لا تصانع. والمداهنة: المصانعة، وهي نوع من النفاق.
(7) تأصلا: تأكد. وأحص: واضبط.
(8) الأعجم: الذي لا يقدر على الكلام أصلاً، والذي لا يفصح ولا يبين كلامه، والذي في لسانه عجمة. والفصيح : البليغ.
(9) جمل : جمع جملة، وهي الكلام.
لا يدخل العول عليها فاعلم ... ... ... ... ثم اسلك التصحيح فيها تسلم
وإن تكن من أصلها تصح ... ... ... ... فترك تطويل الحساب ربح
فأعط كلاً سهمه من أصلها ... ... ... ... مكملاً أو عائلاً من عولها
وإن تر السهام ليست تنقسم ... ... ... ... على ذوي الميراث فاتبع ما رسم
واطلب طريق الاختصار في العمل ... ... بالوفق والضرب يجانبك الزلل(1)
واردد إلى الوفق الذي يوافق ... ... ... واضربه في الأصل فأنت الحاذق(2)
إن كان جنساً واحداً فأكثرا ... ... ... فاحفظ ودع عنك الجدال والمرا(3)
وإن تر الكسر على أجناس ... ... ... ... فإنها في الحكم عند الناس
تحصر في أربعة أقسام ... ... ... ... يعرفها الماهر في الأحكام(4)
مماثل من بعده مناسب ... ... ... ... وبعده موافق مصاحب
والرابع المباين المخالف ... ... ... ... ينبيك عن تفصيلهن العارف
فخذ من المماثلين واحداً ... ... ... ... وخذ من المناسبين الزائدا
واضرب جميع الوفق بالموافق ... ... ... واسلك بذاك أنهج الطرائق(5)
وخذ جميع العدد المباين ... ... ... ... واضربه في الثاني ولا تداهن(6)
فذاك جزء السهم فاعلمنه ... ... ... ... واحذر هديت أن تضل عنه
واضربه في الأصل الذي تأصلا ... ... ... وأحص ما انضم وما تحصلاً(7)
واقسمه فالقسم إذاً صحيح ... ... ... ... يعرفه الأعجم والفصيح(8)
فهذه من الحساب جمل ... ... ... ... يأتي على مثالهن العمل(9)
__________
(1) الزلل : الخطأ.
(2) الحاذق : العارف.
(3) المرا : الجدال والمخاصمة.
(4) الماهر : الحاذق
(5) أنهج الطرائق: أوضح الطرق.
(6) لا تداهن: لا تصانع. والمداهنة: المصانعة، وهي نوع من النفاق.
(7) تأصلا: تأكد. وأحص: واضبط.
(8) الأعجم: الذي لا يقدر على الكلام أصلاً، والذي لا يفصح ولا يبين كلامه، والذي في لسانه عجمة. والفصيح : البليغ.
(9) جمل : جمع جملة، وهي الكلام.
من غير تطويل
ولا اعتساف(1) ... ... ... فاقنع بما بين فهو كاف
الرَّدّ
تعريف الرد:
الرد في اللغة: يطلق على معان؛ منها: الرجوع، والصرف، وعدم القبول.
تقول: رد إليه جواباً: أي رجع.
ورده عن وجهه:أي صرفه.
ورد عليه الشيء، إذا لم يقبله.
والرد اصطلاحاً: نقصان في سهام المسألة، وزيادة في أنصباء الورثة: فهو إذا ضد العول.
فإذا أخذ ذوو الفروض حقوقهم، وبقي شيء من السهام، لا مستحق له، فإنه يرد على جميع ذوي الفروض بقدر حقوقهم، إلا الزوجين، فإنه لا يرد عليهما.
حكم الرد شرعاً:
قلنا سابقاً: إذا كان بيت المال منتظماً بحيث يؤدي الحقوق إلى أصحابها، ويصرف التركة في وجوهها، فإنه لا يرد على أحد من أصحاب الفروض، بل يورث بيت المال، ويقدم على الرد، وعلى ذوي الأرحام، عملاً بقول النبي - صلى الله عليه وسلم - : " من ترك كلاً فإلي، ومن ترك مالاً فلورثته، وأنا وارث من لا وارث له، أعقل عنه وأرثه" رواه أبو داود (2956) بسند صحيح في ( الخراج والإمارة)، باب ( في أرزاق الذرية) عن المقدام بن معدي كرب - رضي الله عنه -.
ومعلوم أنه - صلى الله عليه وسلم - لا يرث لنفسه شيئاً، وإنما ينفق ذلك في مصالح المسلمين.
ومن هنا أفتوا بتوريث بيت المال، وجعلوا مرتبته بعد أصحاب الفروض والعصبات. فإذا لم يكن عصبة، ولم يكن صاحب فرض، أو لم يستغرق أصحاب الفروض بسهامهم جميع التركة، كانت التركة، أو ما فضل منها، من نصيب بيت المال، عملاً بالقاعدة المعروفة: (الغُرْم بالغُنْم).
أما إذا كان بيت المال غير منتظم، فإنه لا حق له في الميراث.
وعندئذ يعمل بالرد على أصحاب الفروض، فإن لم يكونوا، ورث ذوو الأرحام تركة الميت.
هذا وقد أفتى المتأخرون من العلماء، بعدم انتظام بيت المال، بل قالوا: إنه ميئوس من انتظامه حتى ينزل عيسى عليه السلام.
دليل مشروعية الرد:
__________
(1) اعتساف: الأخذ على غير الطريق المستقيم.
الرَّدّ
تعريف الرد:
الرد في اللغة: يطلق على معان؛ منها: الرجوع، والصرف، وعدم القبول.
تقول: رد إليه جواباً: أي رجع.
ورده عن وجهه:أي صرفه.
ورد عليه الشيء، إذا لم يقبله.
والرد اصطلاحاً: نقصان في سهام المسألة، وزيادة في أنصباء الورثة: فهو إذا ضد العول.
فإذا أخذ ذوو الفروض حقوقهم، وبقي شيء من السهام، لا مستحق له، فإنه يرد على جميع ذوي الفروض بقدر حقوقهم، إلا الزوجين، فإنه لا يرد عليهما.
حكم الرد شرعاً:
قلنا سابقاً: إذا كان بيت المال منتظماً بحيث يؤدي الحقوق إلى أصحابها، ويصرف التركة في وجوهها، فإنه لا يرد على أحد من أصحاب الفروض، بل يورث بيت المال، ويقدم على الرد، وعلى ذوي الأرحام، عملاً بقول النبي - صلى الله عليه وسلم - : " من ترك كلاً فإلي، ومن ترك مالاً فلورثته، وأنا وارث من لا وارث له، أعقل عنه وأرثه" رواه أبو داود (2956) بسند صحيح في ( الخراج والإمارة)، باب ( في أرزاق الذرية) عن المقدام بن معدي كرب - رضي الله عنه -.
ومعلوم أنه - صلى الله عليه وسلم - لا يرث لنفسه شيئاً، وإنما ينفق ذلك في مصالح المسلمين.
ومن هنا أفتوا بتوريث بيت المال، وجعلوا مرتبته بعد أصحاب الفروض والعصبات. فإذا لم يكن عصبة، ولم يكن صاحب فرض، أو لم يستغرق أصحاب الفروض بسهامهم جميع التركة، كانت التركة، أو ما فضل منها، من نصيب بيت المال، عملاً بالقاعدة المعروفة: (الغُرْم بالغُنْم).
أما إذا كان بيت المال غير منتظم، فإنه لا حق له في الميراث.
وعندئذ يعمل بالرد على أصحاب الفروض، فإن لم يكونوا، ورث ذوو الأرحام تركة الميت.
هذا وقد أفتى المتأخرون من العلماء، بعدم انتظام بيت المال، بل قالوا: إنه ميئوس من انتظامه حتى ينزل عيسى عليه السلام.
دليل مشروعية الرد:
__________
(1) اعتساف: الأخذ على غير الطريق المستقيم.
يستدل على
مشروعية الرد – بالجملة – بعموم الأولوية، في الأدلة التي قضت بولاية الأرحام
بعضهم لبعض. قال تعالى: { وَأُوْلُواْ الأَرْحَامِ بَعْضُهُمْ أَوْلَى بِبَعْضٍ
فِي كِتَابِ اللّهِ } [ الأنفال: 75].
ولذلك لم يردوا على الزوجين، لأنهما ليسا من ذوي الأرحام ن حيث الزوجية، لأن وصلتهما سببية، وقد انقطعت بالموت.
ومن الأدلة أيضاً في توريث ذوي الأرحام، حديث سعد بن أبي وقاص - رضي الله عنه -، لما أراد أن يوصي بثلثي ماله، فرده النبي - صلى الله عليه وسلم - إلى الثلث وقال له:" إنك أن تذر ورثتك أغنياء خير من أن تذرهم عالة يتكففون الناس" أخرجه البخاري (1233) في (الجنائز)، باب ( رثى النبي سعد بن خولة)؛ ومسلم (1628) في (الوصية)، باب ( الوصية بالثلث). وقد أخبر سعد - رضي الله عنه - النبي - صلى الله عليه وسلم - أنه لا يرثه إلا ابنة له، والبنت فرضها النصف، كما هو معلوم.
فدل ذلك على أن لها حقاً في المال، فيما فوق الفرض، حين لا يوجد معها من يزاحمها، ولا يكون ذلك إلا بالرد.
شروط الرد:
يشترط في الرد، ثلاثة شروط:
وجود صاحب فرض من ورثة الميت، غير الزوجين.
بقاء شيء من التركة، بعد أصحاب الفروض.
عدم وجود عصبة بين الورثة، لأن العصبة يستحق، كل المال بالتعصيب إذا انفرد، أو يأخذ كل ما أبقاه أصحاب الفروض، فلا يتصور الرد مع وجوده.
قاعدة الرد:
لا يخلو حال أصحاب الفروض من أن لا يكون معهم أحد الزوجين، أو أن يكون معهم أحد الزوجين، وإذا فإن موضوع الرد ينقسم إلى حالتين:
الحالة الأولى: أن لا يكون مع من يرد عليه أحد الزوجين:
وفي هذه الحالة نقول:
إذا كان من يرد عليه شخصاً واحداً، كأن مات وخلف بنتاً فقط، فلها كل المال فرضاً، ورداً.
إذا كان من يرد عليه أكثر من واحد، وكانوا صنفاً واحداً، كأن مات، وخلف خمس بنات، فإن المسألة تكون من عدد رؤوسهن، ويقتسمن المال بالسوية.
ولذلك لم يردوا على الزوجين، لأنهما ليسا من ذوي الأرحام ن حيث الزوجية، لأن وصلتهما سببية، وقد انقطعت بالموت.
ومن الأدلة أيضاً في توريث ذوي الأرحام، حديث سعد بن أبي وقاص - رضي الله عنه -، لما أراد أن يوصي بثلثي ماله، فرده النبي - صلى الله عليه وسلم - إلى الثلث وقال له:" إنك أن تذر ورثتك أغنياء خير من أن تذرهم عالة يتكففون الناس" أخرجه البخاري (1233) في (الجنائز)، باب ( رثى النبي سعد بن خولة)؛ ومسلم (1628) في (الوصية)، باب ( الوصية بالثلث). وقد أخبر سعد - رضي الله عنه - النبي - صلى الله عليه وسلم - أنه لا يرثه إلا ابنة له، والبنت فرضها النصف، كما هو معلوم.
فدل ذلك على أن لها حقاً في المال، فيما فوق الفرض، حين لا يوجد معها من يزاحمها، ولا يكون ذلك إلا بالرد.
شروط الرد:
يشترط في الرد، ثلاثة شروط:
وجود صاحب فرض من ورثة الميت، غير الزوجين.
بقاء شيء من التركة، بعد أصحاب الفروض.
عدم وجود عصبة بين الورثة، لأن العصبة يستحق، كل المال بالتعصيب إذا انفرد، أو يأخذ كل ما أبقاه أصحاب الفروض، فلا يتصور الرد مع وجوده.
قاعدة الرد:
لا يخلو حال أصحاب الفروض من أن لا يكون معهم أحد الزوجين، أو أن يكون معهم أحد الزوجين، وإذا فإن موضوع الرد ينقسم إلى حالتين:
الحالة الأولى: أن لا يكون مع من يرد عليه أحد الزوجين:
وفي هذه الحالة نقول:
إذا كان من يرد عليه شخصاً واحداً، كأن مات وخلف بنتاً فقط، فلها كل المال فرضاً، ورداً.
إذا كان من يرد عليه أكثر من واحد، وكانوا صنفاً واحداً، كأن مات، وخلف خمس بنات، فإن المسألة تكون من عدد رؤوسهن، ويقتسمن المال بالسوية.
إذا كان
الورثة الذين يرد عليهم صنفين، فأكثر، كان أصل المسألة من مجموع سهامهم.
وذلك كأن مات شخص، وخلف:
(أصل)
6 ... (رد)
5
6/1 ... أماً ... 1 ... 1
2/1 ... شقيقة ... 3 ... 3
6/1 ... أختاً لأب ... 1 ... 1
فإن أصل هذه المسألة من ستة، لتداخل مخارجها، لكن مجموع سهام الورثة خمسة، فترد المسألة إلى خمسة، ويأخذ كل وارث سهامه من خمسة، فرضاً ورداً، كما هو مرسوم في المسألة السابقة.
الحالة الثانية: أن يكون مع من يرد عليه أحد الزوجين:
وفي هذه الحالة نقول:
نبدأ أولاً بإعطاء الزوج، أو الزوجة فرضه، ونجعل المسألة من مخرج فرض الزوج، أو الزوجة، وهو : اثنان، أو أربعة، أو ثمانية.
ثم يقسم الباقي على من يرد عليه، وفق الترتيب التالي:
1- إذا كان من يرد عليه شخصاً واحداً، كان الباقي بعد فرض الزوجية له. مثاله، ما له خلف شخص:
8
8/1 ... زوجة ... 1
2/1 ... بنتاً ... 7
إذا كان من يرد عليه شخصين، فأكثر، وكانوا من صنف واحد.
فالمسألة كذلك، تكون من مخرج فرض الزوجية، ثم إن انقسم الباقي بعد فرض الزوجية، ثم إن انقسم الباقي بعد فرض الزوجية عليهم فذاك كمن خلفت.
4
4/1 ... زوجاً ... 1
3/2 ... ثلاث بنات ... 3
فأصل المسألة من أربعة، مخرج فرض الزوج، فيأخذ الزوج سهماً واحداً، ويبقى ثلاثة أسهم للبنات، لكل واحدة سهم فرضاً ورداً.
أما إذا لم ينقسم الباقي بعد فرض الزوجية على من يرد عليهم، فلابد والحالة هذه من تصحيح المسألة، وفق القواعد السابقة في التصحيح.
فيضرب أصل المسألة بعدد الرؤوس، إذا كان بين الرؤوس والسهام تباين.
أو يضرب أصل المسألة بوفق الرؤوس إذا كان بين الرؤوس والسهام توافق.
مثال الأول:
(جزء السهم)
3× ... (أصل)
8 ... (تصحيح)
24
8/1 ... زوجة ... 1 ... 3
3/2 ... ثلاث بنات ... 7 ... 21
وذلك كأن مات شخص، وخلف:
(أصل)
6 ... (رد)
5
6/1 ... أماً ... 1 ... 1
2/1 ... شقيقة ... 3 ... 3
6/1 ... أختاً لأب ... 1 ... 1
فإن أصل هذه المسألة من ستة، لتداخل مخارجها، لكن مجموع سهام الورثة خمسة، فترد المسألة إلى خمسة، ويأخذ كل وارث سهامه من خمسة، فرضاً ورداً، كما هو مرسوم في المسألة السابقة.
الحالة الثانية: أن يكون مع من يرد عليه أحد الزوجين:
وفي هذه الحالة نقول:
نبدأ أولاً بإعطاء الزوج، أو الزوجة فرضه، ونجعل المسألة من مخرج فرض الزوج، أو الزوجة، وهو : اثنان، أو أربعة، أو ثمانية.
ثم يقسم الباقي على من يرد عليه، وفق الترتيب التالي:
1- إذا كان من يرد عليه شخصاً واحداً، كان الباقي بعد فرض الزوجية له. مثاله، ما له خلف شخص:
8
8/1 ... زوجة ... 1
2/1 ... بنتاً ... 7
إذا كان من يرد عليه شخصين، فأكثر، وكانوا من صنف واحد.
فالمسألة كذلك، تكون من مخرج فرض الزوجية، ثم إن انقسم الباقي بعد فرض الزوجية، ثم إن انقسم الباقي بعد فرض الزوجية عليهم فذاك كمن خلفت.
4
4/1 ... زوجاً ... 1
3/2 ... ثلاث بنات ... 3
فأصل المسألة من أربعة، مخرج فرض الزوج، فيأخذ الزوج سهماً واحداً، ويبقى ثلاثة أسهم للبنات، لكل واحدة سهم فرضاً ورداً.
أما إذا لم ينقسم الباقي بعد فرض الزوجية على من يرد عليهم، فلابد والحالة هذه من تصحيح المسألة، وفق القواعد السابقة في التصحيح.
فيضرب أصل المسألة بعدد الرؤوس، إذا كان بين الرؤوس والسهام تباين.
أو يضرب أصل المسألة بوفق الرؤوس إذا كان بين الرؤوس والسهام توافق.
مثال الأول:
(جزء السهم)
3× ... (أصل)
8 ... (تصحيح)
24
8/1 ... زوجة ... 1 ... 3
3/2 ... ثلاث بنات ... 7 ... 21
فأصل هذه
المسألة ثمانية، مخرج فرض الزوجة، للزوجة الثمن، وهو سهم واحد، وللبنات الباقي
فرضاً ورداً، وهو سبعة أسهم، وهي غير منقسمة على البنات الثلاث.
فيضرب أصل المسألة بعدد رؤوس البنات، ثلاثة لتباينها مع سهامهن، فتصبح المسألة من (24) ثم يضرب نصيب كل وارث، بجزء السهم، وهو ثلاثة، عدد رؤوس البنات، والحاصل يكون منقسماً على عدد الرؤوس، كما هو مبين في المسألة السابقة.
مثال التوافق:
(جزء السهم)
2× ... (أصل)
4 ... (تصحيح)
8
4/1 ... زوج ... 1 ... 2
3/2 ... ست بنات ... 3 ... 6
أصل هذه المسألة (4)، مخرج فرض الزوج، للزوج الربع، سهم واحد، وللبنات الباقي، ثلاثة أسهم، فرضاً ورداً، وهو غير منقسم عليهن، ولكن بينه وبين عدد رؤوسهن توافق في الثلث، فيؤخذ وفق الرؤوس، وهو اثنان، ويضرب به أصل المسألة، فتصح من ثمانية، ثم يضرب بجزء السهم نصيب كل وارث، فيكون الحاصل منقسماً على عدد الرؤوس. كما بيناه في المسألة السابقة.
إذا كان من يرد عليه أكثر من صنف واحد، فإن كان الباقي بعد فرض الزوجية منقسماً على من يرد عليهن، فذاك، وتصح المسألة من مخرج فرض الزوجية.
مثال ذلك، ما لو مات شخص عن:
4
4/1 ... زوجة ... 1
6/1 ... وأم ... 1
3/1 ... وأخوين لأم ... 2
فالمسألة من أربعة، مخرج فرض من لا يرد عليه، وهي الزوجة، ونصيبها سهم واحد.
ويبقى بعد هذا ثلاثة أسهم، للأم سهم، وللأخوين لأم سهمان، لكل واحد منهما سهم واحد.
أما إذا كان الباقي بعد فرض الزوجية لا ينقسم على من يرد عليهم، فإننا والحالة هذه، نجعل لمن يرد عليهم مسألة مستقلة، ثم ننظر بين مسألتهم، وبين سهامهم من المسألة الأولى، فإن تباينت، ضربنا مسألة الرد، بمسألة الزوجية، فما بلغ فهو الجامعة للمسألتين، ثم نضرب سهام الزوجية بجزء السهم، وهو مسألة الرد، ونضرب سهام من يرد عليهم بجزء السهم، الذي هو نصيب من يرد عليهم من مسألة الزوجية.
ولنضرب لذلك كله مثلاً: مات شخص عن
جزء السهم
فيضرب أصل المسألة بعدد رؤوس البنات، ثلاثة لتباينها مع سهامهن، فتصبح المسألة من (24) ثم يضرب نصيب كل وارث، بجزء السهم، وهو ثلاثة، عدد رؤوس البنات، والحاصل يكون منقسماً على عدد الرؤوس، كما هو مبين في المسألة السابقة.
مثال التوافق:
(جزء السهم)
2× ... (أصل)
4 ... (تصحيح)
8
4/1 ... زوج ... 1 ... 2
3/2 ... ست بنات ... 3 ... 6
أصل هذه المسألة (4)، مخرج فرض الزوج، للزوج الربع، سهم واحد، وللبنات الباقي، ثلاثة أسهم، فرضاً ورداً، وهو غير منقسم عليهن، ولكن بينه وبين عدد رؤوسهن توافق في الثلث، فيؤخذ وفق الرؤوس، وهو اثنان، ويضرب به أصل المسألة، فتصح من ثمانية، ثم يضرب بجزء السهم نصيب كل وارث، فيكون الحاصل منقسماً على عدد الرؤوس. كما بيناه في المسألة السابقة.
إذا كان من يرد عليه أكثر من صنف واحد، فإن كان الباقي بعد فرض الزوجية منقسماً على من يرد عليهن، فذاك، وتصح المسألة من مخرج فرض الزوجية.
مثال ذلك، ما لو مات شخص عن:
4
4/1 ... زوجة ... 1
6/1 ... وأم ... 1
3/1 ... وأخوين لأم ... 2
فالمسألة من أربعة، مخرج فرض من لا يرد عليه، وهي الزوجة، ونصيبها سهم واحد.
ويبقى بعد هذا ثلاثة أسهم، للأم سهم، وللأخوين لأم سهمان، لكل واحد منهما سهم واحد.
أما إذا كان الباقي بعد فرض الزوجية لا ينقسم على من يرد عليهم، فإننا والحالة هذه، نجعل لمن يرد عليهم مسألة مستقلة، ثم ننظر بين مسألتهم، وبين سهامهم من المسألة الأولى، فإن تباينت، ضربنا مسألة الرد، بمسألة الزوجية، فما بلغ فهو الجامعة للمسألتين، ثم نضرب سهام الزوجية بجزء السهم، وهو مسألة الرد، ونضرب سهام من يرد عليهم بجزء السهم، الذي هو نصيب من يرد عليهم من مسألة الزوجية.
ولنضرب لذلك كله مثلاً: مات شخص عن
جزء السهم
(4)
جزء السهم
(3)
مسألة الزوجية
مسألة الرد
الجامعة
4
4
16
4/1
زوجة
1
0
4
2/1
شقيقة
3
3
9
6/1
أخت لأب
1
3
واضح في هذه المسألة أننا ضربنا مسألة الزوجية بمسألة الرد، فكانت الجامعة (16).
ثم ضربنا نصيب الزوجة، بجزء السهم، وهو مسألة الرد.
ثم ضربنا نصيب من يرد عليهم بجزء السهم (3) وهو نصيبهم من مسألة الزوجية.
هذا كله إذا بين مسألة من يرد عليهم وبين نصيبهم من مسألة الزوجية تباين.
أما إذا كان بين مسألتهم، ونصيبهم تماثل، فإن مسألة الزوجية هي الجامعة للمسألتين، لأن نصيب من يرد عليهم من مسألة الزوجية ينقسم عليهم. مثال ذلك: مات رجل عن
مسألة الزوجية
مسألة الرد
الجامعة
4
3
4
4/1
زوجة
1
0
1
6/1
أم
3
1
1
3/1
أختين لأم
2
2
وقد تحتاج مسألة الرد إلى تصحيح، فيجري تصحيحها، ثم يجري بعد التصحيح ما سبق وذكرناه. مثال ذلك: مات شخص عن
(جزء السهم)
(3)
مسألة الزوجية
مسألة الرد
الجامعة
التصحيح
4
3
4
12
4/1
زوجة
1
0
1
3
6/1
أم
3
1
1
3
3/1
ثلاث أخوات لأم
2
2
6
واضح في المسألة أن نصيب من يرد عليهم من مسألة الزوجية منقسم عليهم، لذلك جعلنا الجامعة هي مسألة الزوجية.
لكن نصيب الأخوات لأم، وهو (2) من الجامعة غير منقسم على عدد رؤوسهن، وهو (3)، فصححنا الجامعة، وذلك بضرب الجامعة بعدد رؤوس الأخوات لأم، لأن نصيبهن، وهو (2) يباين عدد رؤوسهن، فكان نصيبهن بعد التصحيح منقسماً عليهن، وهو لكل أخت سهمان.
المناسخات
تعريف المناسخات:
المناسخات في اللغة: جمع مناسخة، ومناسخة مصدر، وإنما جمع لاختلاف أنواع المناسخة، والأصل في المصدر، انه لا يثني، ولا يجمع.
والمناسخة مأخوذة من النسخ.
والنسخ لغة يطبق على معان، منها:
الإزالة، تقول: نسخت الشمس الظل، وانتسخته: أي إزالته.
والتغيير، يقال: نسخت الريح آثار الديار، إذا غيرتها.
والنقل، تقول: نسخت الكتاب، وانتسخته، واستنسخته إذا نقلت ما فيه باللفظ والمعنى نقلاً صحيحاً.
جزء السهم
(3)
مسألة الزوجية
مسألة الرد
الجامعة
4
4
16
4/1
زوجة
1
0
4
2/1
شقيقة
3
3
9
6/1
أخت لأب
1
3
واضح في هذه المسألة أننا ضربنا مسألة الزوجية بمسألة الرد، فكانت الجامعة (16).
ثم ضربنا نصيب الزوجة، بجزء السهم، وهو مسألة الرد.
ثم ضربنا نصيب من يرد عليهم بجزء السهم (3) وهو نصيبهم من مسألة الزوجية.
هذا كله إذا بين مسألة من يرد عليهم وبين نصيبهم من مسألة الزوجية تباين.
أما إذا كان بين مسألتهم، ونصيبهم تماثل، فإن مسألة الزوجية هي الجامعة للمسألتين، لأن نصيب من يرد عليهم من مسألة الزوجية ينقسم عليهم. مثال ذلك: مات رجل عن
مسألة الزوجية
مسألة الرد
الجامعة
4
3
4
4/1
زوجة
1
0
1
6/1
أم
3
1
1
3/1
أختين لأم
2
2
وقد تحتاج مسألة الرد إلى تصحيح، فيجري تصحيحها، ثم يجري بعد التصحيح ما سبق وذكرناه. مثال ذلك: مات شخص عن
(جزء السهم)
(3)
مسألة الزوجية
مسألة الرد
الجامعة
التصحيح
4
3
4
12
4/1
زوجة
1
0
1
3
6/1
أم
3
1
1
3
3/1
ثلاث أخوات لأم
2
2
6
واضح في المسألة أن نصيب من يرد عليهم من مسألة الزوجية منقسم عليهم، لذلك جعلنا الجامعة هي مسألة الزوجية.
لكن نصيب الأخوات لأم، وهو (2) من الجامعة غير منقسم على عدد رؤوسهن، وهو (3)، فصححنا الجامعة، وذلك بضرب الجامعة بعدد رؤوس الأخوات لأم، لأن نصيبهن، وهو (2) يباين عدد رؤوسهن، فكان نصيبهن بعد التصحيح منقسماً عليهن، وهو لكل أخت سهمان.
المناسخات
تعريف المناسخات:
المناسخات في اللغة: جمع مناسخة، ومناسخة مصدر، وإنما جمع لاختلاف أنواع المناسخة، والأصل في المصدر، انه لا يثني، ولا يجمع.
والمناسخة مأخوذة من النسخ.
والنسخ لغة يطبق على معان، منها:
الإزالة، تقول: نسخت الشمس الظل، وانتسخته: أي إزالته.
والتغيير، يقال: نسخت الريح آثار الديار، إذا غيرتها.
والنقل، تقول: نسخت الكتاب، وانتسخته، واستنسخته إذا نقلت ما فيه باللفظ والمعنى نقلاً صحيحاً.
والنسخ شرعاً:
رفع حكم شرعي، فإثبات حكم آخر مكانه، كنسخ استقبال بيت المقدس في الصلاة، باستقبال
الكعبة.
والمناسخة في اصطلاح علم الفرائض: أن يموت من ورثة الميت الأول واحد، أو أكثر، قبل قسمة التركة، سميت مناسخة، لأن المسألة الأولى، انتسخت بالثانية، أو لأن المال ينتقل فيها من وارث إلى وارث.
ومن هنا يظهر لك مناسبة المعنى الاصطلاحي، للمعنى اللغوي.
تقسيم التركة في مسائل المناسخات:
إذا مات شخص، ثم مات من ورثته شخص آخر قبل قسمة تركته، لزم اتباع الخطوات التالية:
يجعل للميت الأول مسألة مستقلة، يحصى فيها ورثته، ونصيب كل وارث منهم، حسب ما تقدم في عمل المسائل.
تصحيح مسألة الميت الأول، إن احتاجت إلى تصحيح، وفق القواعد السابقة في تصحيح المسائل.
يجعل للميت الثاني مسألة مستقلة، يحصى فيها ورثته، سواء كانوا من ورثة الميت الأول، أو من غيرهم، ويحصى نصيب كل واحد منهم من تركة الميت الثاني.
تصحيح مسألة الميت الثاني إن احتاجت إلى تصحيح.
النظر بين سهام الميت الثاني التي ورثها من الميت الأول، وبين أصل مسألته، أو تصحيحها.
فإن ما ثلث سهامه أصل مسألته، أو تصحيحها، صحت الجامعة للمسألتين مما صحت منه المسألة الأولى.
وإن وافقت سهامه التي ورثها من المسألة الأولى أصل مسألته، أو تصحيحها، أخذنا وفق مسألته وضربنا به أصل المسألة الأولى، أو تصحيحها، فما بلغ فهو الجامعة للمسألتين.
وإذا باينت سهام الميت الثاني أصل مسألته، أو تصحيحها، ضربنا أصل المسألة الأولى، أو تصحيحها، بأصل المسألة الثانية أو تصحيحها، وكان هذا الضرب هو الجامعة للمسألتين.
النظر إلى الورثة في المسألتين:
فمن ورث منهم من المسألة الأولى فقط، أخذ نصيبه مضروباً بوفق المسألة الثانية، عند التوافق، أو بكاملها عند التباين.
ومن ورث منهم من المسألة الثانية فقط، أخذ نصيبه مضروباً ، بوفق سهام الميت الثاني عند التوافق، أو بكاملها عند التباين.
والمناسخة في اصطلاح علم الفرائض: أن يموت من ورثة الميت الأول واحد، أو أكثر، قبل قسمة التركة، سميت مناسخة، لأن المسألة الأولى، انتسخت بالثانية، أو لأن المال ينتقل فيها من وارث إلى وارث.
ومن هنا يظهر لك مناسبة المعنى الاصطلاحي، للمعنى اللغوي.
تقسيم التركة في مسائل المناسخات:
إذا مات شخص، ثم مات من ورثته شخص آخر قبل قسمة تركته، لزم اتباع الخطوات التالية:
يجعل للميت الأول مسألة مستقلة، يحصى فيها ورثته، ونصيب كل وارث منهم، حسب ما تقدم في عمل المسائل.
تصحيح مسألة الميت الأول، إن احتاجت إلى تصحيح، وفق القواعد السابقة في تصحيح المسائل.
يجعل للميت الثاني مسألة مستقلة، يحصى فيها ورثته، سواء كانوا من ورثة الميت الأول، أو من غيرهم، ويحصى نصيب كل واحد منهم من تركة الميت الثاني.
تصحيح مسألة الميت الثاني إن احتاجت إلى تصحيح.
النظر بين سهام الميت الثاني التي ورثها من الميت الأول، وبين أصل مسألته، أو تصحيحها.
فإن ما ثلث سهامه أصل مسألته، أو تصحيحها، صحت الجامعة للمسألتين مما صحت منه المسألة الأولى.
وإن وافقت سهامه التي ورثها من المسألة الأولى أصل مسألته، أو تصحيحها، أخذنا وفق مسألته وضربنا به أصل المسألة الأولى، أو تصحيحها، فما بلغ فهو الجامعة للمسألتين.
وإذا باينت سهام الميت الثاني أصل مسألته، أو تصحيحها، ضربنا أصل المسألة الأولى، أو تصحيحها، بأصل المسألة الثانية أو تصحيحها، وكان هذا الضرب هو الجامعة للمسألتين.
النظر إلى الورثة في المسألتين:
فمن ورث منهم من المسألة الأولى فقط، أخذ نصيبه مضروباً بوفق المسألة الثانية، عند التوافق، أو بكاملها عند التباين.
ومن ورث منهم من المسألة الثانية فقط، أخذ نصيبه مضروباً ، بوفق سهام الميت الثاني عند التوافق، أو بكاملها عند التباين.
ومن ورث منهم
من المسألتين، أخذه مضروباً في الأولى بوفق الثانية عند التوافق، أو بكاملها عند
التباين، وأخذ نصيبه من الثانية،مضروباً بوفق سهام الميت الثاني عند الموافقة، أو
بكاملها عند التباين، ثم يجمع له النصيبان، ويأخذهما من الجامعة.
وإليك الأمثلة الموضحة لهذه القواعد
المثال الأول: إذا كانت سهام الميت الثاني مماثلة لمسألته:
ماتت امرأة عن زوج، وأم، وعم، ثم مات الزوج قبل قسمة التركة عن ثلاثة أبناء.
الحل:
أصل
المسألة الأولى ... أصل
المسألة الثانية ... الجامعة
6 ... 3 ... 6
2/1 ... زوج ... 3 ... ت
3/1 ... أم ... 2 ... غريبة ... 2
ع ... عم ... 1 ... غريب ... 1
ع ثلاثة أبناء ... 3
واضح في هذه المسألة أن الزوج ورث من زوجته النصف لعدم وجود الفرع الوارث لها، وأن الأم ورثت الثلث لعدم الفرع الوارث، وعدم العدد من الإخوة، وأن العم ورث الباقي بالتعصيب.
وواضح أيضاً أن أصل المسألة (6) لأن مخرجيها: (2و3) متباينان، فضرب أحدهما بالآخر، فكان أصل المسألة، وهو (6).
وعليه فإن نصيب الزوج (3) أسهم، ونصيب الأم (2) ونصيب العم (1).
أما المسألة الثانية، فإن الميت إنما هو الزوج، وقد خلف ثلاثة بنين. هم ورثته بالتعصيب، وأصل مسألتهم (3) من عدد رؤوسهم.
ولما نظرنا بين مسألة الميت الثاني وهو الزوج وبين سهامه التي ورثها من الميت الأول رأينا بينهما تماثلاً.
وعليه فقد صححنا الجامعة من أصل المسألة الأولى وأعطينا كل وارث نصيبه منها، كما هو موضح في المسألة السابقة.
مثال آخر:
ماتت امرأة عن زوج وأختين لأب، ثم ماتت إحدى الأختين، عمن ذكر، وعن بني.
الحل
أصل
المسألة الأولى
أصل
المسألة الثانية
الجامعة
7 (عول)
6
2
7
2/1
زوج
3
3
3/2
أخت لأب
2
ع
أخت لأب
1
3
أخت لأب
2
ت
2/1
بنت
1
1
هذه المسألة مثل سابقتها، كانت سهام الميت الثاني، وهي الأخت، مماثلة لمسألتها، فصحت الجامعة مما صحت منه المسألة الأولى.
وإليك الأمثلة الموضحة لهذه القواعد
المثال الأول: إذا كانت سهام الميت الثاني مماثلة لمسألته:
ماتت امرأة عن زوج، وأم، وعم، ثم مات الزوج قبل قسمة التركة عن ثلاثة أبناء.
الحل:
أصل
المسألة الأولى ... أصل
المسألة الثانية ... الجامعة
6 ... 3 ... 6
2/1 ... زوج ... 3 ... ت
3/1 ... أم ... 2 ... غريبة ... 2
ع ... عم ... 1 ... غريب ... 1
ع ثلاثة أبناء ... 3
واضح في هذه المسألة أن الزوج ورث من زوجته النصف لعدم وجود الفرع الوارث لها، وأن الأم ورثت الثلث لعدم الفرع الوارث، وعدم العدد من الإخوة، وأن العم ورث الباقي بالتعصيب.
وواضح أيضاً أن أصل المسألة (6) لأن مخرجيها: (2و3) متباينان، فضرب أحدهما بالآخر، فكان أصل المسألة، وهو (6).
وعليه فإن نصيب الزوج (3) أسهم، ونصيب الأم (2) ونصيب العم (1).
أما المسألة الثانية، فإن الميت إنما هو الزوج، وقد خلف ثلاثة بنين. هم ورثته بالتعصيب، وأصل مسألتهم (3) من عدد رؤوسهم.
ولما نظرنا بين مسألة الميت الثاني وهو الزوج وبين سهامه التي ورثها من الميت الأول رأينا بينهما تماثلاً.
وعليه فقد صححنا الجامعة من أصل المسألة الأولى وأعطينا كل وارث نصيبه منها، كما هو موضح في المسألة السابقة.
مثال آخر:
ماتت امرأة عن زوج وأختين لأب، ثم ماتت إحدى الأختين، عمن ذكر، وعن بني.
الحل
أصل
المسألة الأولى
أصل
المسألة الثانية
الجامعة
7 (عول)
6
2
7
2/1
زوج
3
3
3/2
أخت لأب
2
ع
أخت لأب
1
3
أخت لأب
2
ت
2/1
بنت
1
1
هذه المسألة مثل سابقتها، كانت سهام الميت الثاني، وهي الأخت، مماثلة لمسألتها، فصحت الجامعة مما صحت منه المسألة الأولى.
غير أن هذه
المسألة فيها عول، وأن إحدى الأختين ورثت من أختها الأولى، ومن أختها الثانية.
ومعلوم أن الأخت مع البنت تعتبر عصبة مع الغير، كما هو مبين في المسألة الثانية.
المثال الثاني: إذا كانت سهام الميت الثاني موافقة لمسألته:
ماتت امرأة عن زوج، وأم، وعم، ثم مات الزوج عن أم، وأخوين لأم، وأخ لأب.
الحل:
المسألة الأولى
المسألة الثانية
الجامعة
6
6
12
2/1
زوج
3
ت
3/1
أم
2
غريبة
4
ع
عم
1
غريب
2
6/1
أم
1
1
3/1
أخوان لأم
2
2
ع
أخ لأب
3
3
لقد قسمنا سهام المسألة الأولى على ورثتها، وقسمنا سهم المسألة الثانية أيضاً على ورثتها، ثم نظرنا بين سهام الميت الثاني، وهو الزوج، وبين مسألته، فإذا هما متوافقان في الثلث، فأخذنا ثلث المسألة الثانية (2)، وهو وفقها، وضربنا به كامل المسألة الأولى (6) فكانت الجامعة (12)، ثم من ورث من المسألة الأولى، ضربنا نصيبه بوفق الثانية، فكان نصيب الأم (2×2=4)، ونصيب العم (1×2=2)، ووضعنا ذلك تحت الجامعة.
ومن ورث من المسألة الثانية ضربنا نصيبه بوفق سهام الميت، وهو(1)، فكان نصيب الأم في المسألة الثانية (1×1=1)، ونصيب الأخوين لأم ( 2×1=2)، ونصيب الأخ لأب (3×1=3)، ووضعنا ذلك تحت الجامعة أيضاً، ولو جمعنا سهام الورثة في الجامعة، لوجدناها مساوية للجامعة، وهذا دليل صحة عملنا.
مثال آخر:
مات رجل عن أب، وأم، وبنت، وابن، ثم مات الابن قبل قسمة التركة عن المذكورين وعن زوجة، وابن.
الحل:
أصل
تصحيح
المسألة الثانية
الجامعة
6
18
24
54
6/1
أب
1
3
6/1
جد
4
13
6/1
أم
1
3
6/1
جدة
4
13
ع
بنت
4
4
م
شقيقة
0
12
ابن
8
ت
8/1
زوجة
3
3
ع
ابن
13
13
ومعلوم أن الأخت مع البنت تعتبر عصبة مع الغير، كما هو مبين في المسألة الثانية.
المثال الثاني: إذا كانت سهام الميت الثاني موافقة لمسألته:
ماتت امرأة عن زوج، وأم، وعم، ثم مات الزوج عن أم، وأخوين لأم، وأخ لأب.
الحل:
المسألة الأولى
المسألة الثانية
الجامعة
6
6
12
2/1
زوج
3
ت
3/1
أم
2
غريبة
4
ع
عم
1
غريب
2
6/1
أم
1
1
3/1
أخوان لأم
2
2
ع
أخ لأب
3
3
لقد قسمنا سهام المسألة الأولى على ورثتها، وقسمنا سهم المسألة الثانية أيضاً على ورثتها، ثم نظرنا بين سهام الميت الثاني، وهو الزوج، وبين مسألته، فإذا هما متوافقان في الثلث، فأخذنا ثلث المسألة الثانية (2)، وهو وفقها، وضربنا به كامل المسألة الأولى (6) فكانت الجامعة (12)، ثم من ورث من المسألة الأولى، ضربنا نصيبه بوفق الثانية، فكان نصيب الأم (2×2=4)، ونصيب العم (1×2=2)، ووضعنا ذلك تحت الجامعة.
ومن ورث من المسألة الثانية ضربنا نصيبه بوفق سهام الميت، وهو(1)، فكان نصيب الأم في المسألة الثانية (1×1=1)، ونصيب الأخوين لأم ( 2×1=2)، ونصيب الأخ لأب (3×1=3)، ووضعنا ذلك تحت الجامعة أيضاً، ولو جمعنا سهام الورثة في الجامعة، لوجدناها مساوية للجامعة، وهذا دليل صحة عملنا.
مثال آخر:
مات رجل عن أب، وأم، وبنت، وابن، ثم مات الابن قبل قسمة التركة عن المذكورين وعن زوجة، وابن.
الحل:
أصل
تصحيح
المسألة الثانية
الجامعة
6
18
24
54
6/1
أب
1
3
6/1
جد
4
13
6/1
أم
1
3
6/1
جدة
4
13
ع
بنت
4
4
م
شقيقة
0
12
ابن
8
ت
8/1
زوجة
3
3
ع
ابن
13
13
في هذه
المسألة، نجد أن الأب ورث من المسألة الأولى السدس، والأم ورثت أيضاً السدس، وورث
الابن والبنت الباقي تعصيباً، فكان أصل المسألة (6) لتماثل مخرج فرض الأب والأم،
للأب سهم واحد، وللأم سهم، وللبنت والابن الباقي وهو أربعة أسهم، للذكر مثل حظ
الأنثيين، صرنا إلى تصحيح المسألة.
ولما كان بين عدد الرؤوس والسهام تباين المسألة (6) بعدد الرؤوس (3) فكان تصحيح المسألة (18). أما المسألة الثانية، فقد أصبح الأب فيها جداً، وأصبحت الأم جدة، والبنت أختاً شقيقة، ثم ورث الجد السدس، والجدة السدس، والأخت الشقيقة محجوبة بالابن، والزوجة ورثت الثمن، والابن أخذ الباقي بالتعصيب.
وأصل المسألة الثانية (24) لأن بين مخرج فرض الزوجة، ومخرج فرض الأب، أو الأم توافقاً بالنصف، فضربنا وفق أحدهما بكامل الآجر: (4×6=24) فكان أصل المسألة.
للجد (4) أسهم، وللجدة (4) أسهم، وللزوجة (3) أسهم، وللابن (13) سهماً.
ثم بعد كل هذا يأتي دور الجامعة للمسألتين وهنا يجب أن ننظر بين سهام الميت الثاني التي ورثها من الميت الأول، وبين مسألته، وعندئذ سنجدهما متوافقين في الثمن.
فإذا أخذنا ثمن المسألة الثانية، وضربنا به تصحيح المسألة الأولى،
كان الحاصل (54) هو الجامعة: (15×3=54).
ثم نأخذ وفق المسألة الثانية، ونجعله جزء سهم عند الأولى لنضرب به نصيب كل وارث من المسألة الأولى ونأخذ وفق سهام الميت الثاني ونجعله جزء سهم عند المسألة الثانية، لنضرب به نصيب كل وارث من المسألة الثانية، ومن ورث من المسألتين جمعنا له نصيبه منهما، ووضعناه تحت الجامعة.
وبهذا نكون قد وصلنا إلى حل لهذه المسألة، وأخذ كل وارث نصيبه، كما هو مبين في المسألة.
المثال الثالث: إذا كانت سهام الميت الثاني مباينة لمسألته:
ماتت امرأة عن زوج، وأم، وعم، ثم مات الزوج عن بنت، وخمسة أشقاء.
المسألة الأولى ... المسألة الثانية ... تصحيح الثانية ... الجامعة
6 ... 2 ... 10 ... 60
ولما كان بين عدد الرؤوس والسهام تباين المسألة (6) بعدد الرؤوس (3) فكان تصحيح المسألة (18). أما المسألة الثانية، فقد أصبح الأب فيها جداً، وأصبحت الأم جدة، والبنت أختاً شقيقة، ثم ورث الجد السدس، والجدة السدس، والأخت الشقيقة محجوبة بالابن، والزوجة ورثت الثمن، والابن أخذ الباقي بالتعصيب.
وأصل المسألة الثانية (24) لأن بين مخرج فرض الزوجة، ومخرج فرض الأب، أو الأم توافقاً بالنصف، فضربنا وفق أحدهما بكامل الآجر: (4×6=24) فكان أصل المسألة.
للجد (4) أسهم، وللجدة (4) أسهم، وللزوجة (3) أسهم، وللابن (13) سهماً.
ثم بعد كل هذا يأتي دور الجامعة للمسألتين وهنا يجب أن ننظر بين سهام الميت الثاني التي ورثها من الميت الأول، وبين مسألته، وعندئذ سنجدهما متوافقين في الثمن.
فإذا أخذنا ثمن المسألة الثانية، وضربنا به تصحيح المسألة الأولى،
كان الحاصل (54) هو الجامعة: (15×3=54).
ثم نأخذ وفق المسألة الثانية، ونجعله جزء سهم عند الأولى لنضرب به نصيب كل وارث من المسألة الأولى ونأخذ وفق سهام الميت الثاني ونجعله جزء سهم عند المسألة الثانية، لنضرب به نصيب كل وارث من المسألة الثانية، ومن ورث من المسألتين جمعنا له نصيبه منهما، ووضعناه تحت الجامعة.
وبهذا نكون قد وصلنا إلى حل لهذه المسألة، وأخذ كل وارث نصيبه، كما هو مبين في المسألة.
المثال الثالث: إذا كانت سهام الميت الثاني مباينة لمسألته:
ماتت امرأة عن زوج، وأم، وعم، ثم مات الزوج عن بنت، وخمسة أشقاء.
المسألة الأولى ... المسألة الثانية ... تصحيح الثانية ... الجامعة
6 ... 2 ... 10 ... 60
2/1 ... زوج
... 3 ... ت
3/1 ... أم ... 2 ... - ... 20
ع ... عم ... 1 ... - ... 10
2/1 ... بنت ... 1 ... 5 ... 15
ع ... 5 أشقاء ... 1 ... 5 ... 15
يتضح لنا في هذه المسألة، أن بين سهام الميت الثاني من المسألة الأولى، وهي (3) وبين مسألته، وهي (10)، تبايناً، لذلك ضربنا أصل المسألة الأولى بتصحيح المسألة الثانية، فكانت الجامعة: ( 6×10=60).
ويلاحظ في المسألة الثانية أننا قد أجرينا فيها تصحيحاً، وذلك لأن سهام الإخوة لا تنقسم عليهم، وبين سهامهم ورؤوسهم تباين، فضربنا أصل المسألة (2) بعدد الرؤوس (5) فكان التصحيح (10)، ثم إنه من كان له نصيب في المسألة الأولى أخذه مضروباً بتصحيح المسألة الثانية، فنصيب الأم (2×10=20)، ونصيب العم (1×10=10)، فوضعناه تحت الجامعة. ومن كان له نصيب في المسألة الثانية أخذه مضروباً بسهام الميت الثاني التي ورثها من الميت الأول، فكان نصيب البنت (5×3=15)، ونصيب الأشقاء ( 5×3=15)، فوضعنا ذلك تحت الجامعة أيضاً.
وعند مراجعة السهام كلها في الجامعة، وجمعها مع بعضها وجدناها مساوية للجامعة، وهذا دليل صحة التقسيم في هذه المسألة.
مثال آخر:
مات رجل عن زوجة، وثلاثة أبناء، وبنت، ثم ماتت البنت، عن الورثة في المسألة السابقة.
المسألة الأولى
المسألة الثانية
تصحيح الثانية
الجامعة
8
6
18
144
8/1
زوجة
1
6/1
أم
1
3
21
ع
ابن
2
ع
شقيق
5
5
41
ابن
2
شقيق
5
41
ابن
2
شقيق
5
41
بنت
1
ت
واضح من حل هذه المسألة أن الأولى صحت من (8) والثانية من (18)، ونصيب الميت الثاني من المسألة الأولى سهم واحد، وهو يباين مسألته، فنضرب المسألة الثانية في الأولى، فتبلغ (144) هي الجامعة للمسألتين.
3/1 ... أم ... 2 ... - ... 20
ع ... عم ... 1 ... - ... 10
2/1 ... بنت ... 1 ... 5 ... 15
ع ... 5 أشقاء ... 1 ... 5 ... 15
يتضح لنا في هذه المسألة، أن بين سهام الميت الثاني من المسألة الأولى، وهي (3) وبين مسألته، وهي (10)، تبايناً، لذلك ضربنا أصل المسألة الأولى بتصحيح المسألة الثانية، فكانت الجامعة: ( 6×10=60).
ويلاحظ في المسألة الثانية أننا قد أجرينا فيها تصحيحاً، وذلك لأن سهام الإخوة لا تنقسم عليهم، وبين سهامهم ورؤوسهم تباين، فضربنا أصل المسألة (2) بعدد الرؤوس (5) فكان التصحيح (10)، ثم إنه من كان له نصيب في المسألة الأولى أخذه مضروباً بتصحيح المسألة الثانية، فنصيب الأم (2×10=20)، ونصيب العم (1×10=10)، فوضعناه تحت الجامعة. ومن كان له نصيب في المسألة الثانية أخذه مضروباً بسهام الميت الثاني التي ورثها من الميت الأول، فكان نصيب البنت (5×3=15)، ونصيب الأشقاء ( 5×3=15)، فوضعنا ذلك تحت الجامعة أيضاً.
وعند مراجعة السهام كلها في الجامعة، وجمعها مع بعضها وجدناها مساوية للجامعة، وهذا دليل صحة التقسيم في هذه المسألة.
مثال آخر:
مات رجل عن زوجة، وثلاثة أبناء، وبنت، ثم ماتت البنت، عن الورثة في المسألة السابقة.
المسألة الأولى
المسألة الثانية
تصحيح الثانية
الجامعة
8
6
18
144
8/1
زوجة
1
6/1
أم
1
3
21
ع
ابن
2
ع
شقيق
5
5
41
ابن
2
شقيق
5
41
ابن
2
شقيق
5
41
بنت
1
ت
واضح من حل هذه المسألة أن الأولى صحت من (8) والثانية من (18)، ونصيب الميت الثاني من المسألة الأولى سهم واحد، وهو يباين مسألته، فنضرب المسألة الثانية في الأولى، فتبلغ (144) هي الجامعة للمسألتين.
للزوجة من
المسألة الأولى (1) يضرب في (18) يساوي (18)، ولها من الثانية، باعتبارها أماً،
(3) تضرب بواحد، وهو نصيب الميت الثاني من الأولى، يساوي ثلاثة. ولكل ابن من
المسألة الأولى سهمان، يضربان بـ (18) فيحصل لكل واحد (36) سهماً من الأولى، ولكل
واحد منهم باعتبارهم أخوة أشقاء من المسألة الثانية (5) أسهم تضرب بواحد، تساوي
خمسة، ثم يجمع نصيب كل واحد من المسألتين، فيكون الناتج هكذا:
الأم: (18 + 3 = 21)
الابن: ( 36 + 5 = 41)
الابن: ( 36 + 5 = 41)
الابن: ( 36 + 5 = 41)
كما هو مبين في المسألة السابقة.
كان ما مر في المناسخات كله إنما هو فيما إذا مات من ورثة الميت الأول شخص واحد.
فإذا مات شخص ثان قبل قسمة التركة، فإن العمل أن نجعل الجامعة الأولى كمسألة أولى، ونجعل للميت الثالث مسألة جديدة وتطبق بين مسألة الميت الثالث والجامعة نفس القواعد التي مر ذكرها في الميت الأول والثاني، فلا حاجة لإعادتها.
هذا ومما ينبغي أن يعلم أنه إذا كان لا يرث الميت الثاني إلا الباقون من ورثة الميت الأول، وكان إرثهم من الميت الثاني كإرثهم من الميت الأول، جعل كأن الميت الثاني لم يكن من ورثة الميت الأول، وقسم المال المتروك بين الباقين من الورثة، لأنه صار إليهم بطريق واحد.
مثال هذا:
ما لو مات شخص عن أربعة إخوة أشقاء، ثم مات واحد منهم عن الباقين من الإخوة، ثم مات ثالث عن الباقين أنفسهم، فإننا نعتبر الذين ماتوا بعد الأول كأنهم لم يكونوا، وتقسم التركة على الباقين منهم.
قال الإمام الرحبي رحمه الله تعالى، في ( المناسخات):
وإن يمت آخر قبل القسمة ... ... ... ... فصحح الحساب واعرف سهمه
واجعل له مسالة أخرى كما ... ... ... ... قد بين التفصيل فيما قدما
وإن تكن ليست عليها تنقسم ... ... ... ... فارجع إلى الوفق بهذا قد حكم
الأم: (18 + 3 = 21)
الابن: ( 36 + 5 = 41)
الابن: ( 36 + 5 = 41)
الابن: ( 36 + 5 = 41)
كما هو مبين في المسألة السابقة.
كان ما مر في المناسخات كله إنما هو فيما إذا مات من ورثة الميت الأول شخص واحد.
فإذا مات شخص ثان قبل قسمة التركة، فإن العمل أن نجعل الجامعة الأولى كمسألة أولى، ونجعل للميت الثالث مسألة جديدة وتطبق بين مسألة الميت الثالث والجامعة نفس القواعد التي مر ذكرها في الميت الأول والثاني، فلا حاجة لإعادتها.
هذا ومما ينبغي أن يعلم أنه إذا كان لا يرث الميت الثاني إلا الباقون من ورثة الميت الأول، وكان إرثهم من الميت الثاني كإرثهم من الميت الأول، جعل كأن الميت الثاني لم يكن من ورثة الميت الأول، وقسم المال المتروك بين الباقين من الورثة، لأنه صار إليهم بطريق واحد.
مثال هذا:
ما لو مات شخص عن أربعة إخوة أشقاء، ثم مات واحد منهم عن الباقين من الإخوة، ثم مات ثالث عن الباقين أنفسهم، فإننا نعتبر الذين ماتوا بعد الأول كأنهم لم يكونوا، وتقسم التركة على الباقين منهم.
قال الإمام الرحبي رحمه الله تعالى، في ( المناسخات):
وإن يمت آخر قبل القسمة ... ... ... ... فصحح الحساب واعرف سهمه
واجعل له مسالة أخرى كما ... ... ... ... قد بين التفصيل فيما قدما
وإن تكن ليست عليها تنقسم ... ... ... ... فارجع إلى الوفق بهذا قد حكم
وانظر فإن
وافقت السهاما ... ... ... ... فخذ هديت وفقها تماما(1)
واضربه أو جميعها في السابقة ... ... ... إن لم تكن بينهما موافقة
وكل سهم في جميع الثانية ... ... ... ... يضرب أو في وفقها علانية(2)
وأسهم الأخرى ففي السهام ... ... ... ... تضرب أو في وفقها تمام
فهذه طريقة المناسخة ... ... ... ... ... فارق بها رتبة فضل شامخة(3)
توريث ذوي الأرحام
تعريف ذوي الأرحام:
الأرحام: جمع رحم، والرحم لغة: القرابة، وذو الأرحام: أصحاب القرابات.
وذوو الأرحام في اصطلاح علم الفرائض هم : كل قريب لا يرث بفرض، ولا تعصيب، أي هم من عدا الأقارب المجمع على توريثهم، ممن سبق ذكرهم في هذا الكتاب.
شروط توريث ذوي الأرحام:
يشترط في إرث ذوي الأرحام الشروط التالية:
أ- أن لا يوجد للميت وارث بفرض أو تعصيب، ما عدا الزوجين.
فإذا كان له وارث من أصحاب الفروض، أو العصبات، فهو مقدم على ذوي الأرحام، بالفرض، والتعصيب والرد.
أما وجود أحد الزوجين، فلا يمنع من توريث ذوي الأرحام، إذا لم يكن وارث غيره، لأنه لا يرد على الزوجين، كما سبق بيانه.
ب- أن لا يكون بيت المال منتظماً، فإذا كان بيت المال منتظماً، فإنه مقدم على ذوي الأرحام في الميراث، كما هو مقدم على الرد على ذوي الفروض، وقد سبق بيان ذلك.
دليل عدم توريثهم إذا كان بيت المال منتظماً:
استدل الشافعي رحمه الله تعالى على عدم توريثهم أنه لم يرد لهم نصيب معين من الميراث، في القرآن ولا في السنة، ولو كان لهم حق في التركة لبينه الله عز وجل، ورسوله عليه الصلاة والسلام، كما هو الشأن في أصحاب الفروض، والعصبات.
__________
(1) هديت جملة دعائية. والهداية: الدلالة على الخير.
(2) علانية : جهراً.
(3) شامخة: مرتفعة عالية.
واضربه أو جميعها في السابقة ... ... ... إن لم تكن بينهما موافقة
وكل سهم في جميع الثانية ... ... ... ... يضرب أو في وفقها علانية(2)
وأسهم الأخرى ففي السهام ... ... ... ... تضرب أو في وفقها تمام
فهذه طريقة المناسخة ... ... ... ... ... فارق بها رتبة فضل شامخة(3)
توريث ذوي الأرحام
تعريف ذوي الأرحام:
الأرحام: جمع رحم، والرحم لغة: القرابة، وذو الأرحام: أصحاب القرابات.
وذوو الأرحام في اصطلاح علم الفرائض هم : كل قريب لا يرث بفرض، ولا تعصيب، أي هم من عدا الأقارب المجمع على توريثهم، ممن سبق ذكرهم في هذا الكتاب.
شروط توريث ذوي الأرحام:
يشترط في إرث ذوي الأرحام الشروط التالية:
أ- أن لا يوجد للميت وارث بفرض أو تعصيب، ما عدا الزوجين.
فإذا كان له وارث من أصحاب الفروض، أو العصبات، فهو مقدم على ذوي الأرحام، بالفرض، والتعصيب والرد.
أما وجود أحد الزوجين، فلا يمنع من توريث ذوي الأرحام، إذا لم يكن وارث غيره، لأنه لا يرد على الزوجين، كما سبق بيانه.
ب- أن لا يكون بيت المال منتظماً، فإذا كان بيت المال منتظماً، فإنه مقدم على ذوي الأرحام في الميراث، كما هو مقدم على الرد على ذوي الفروض، وقد سبق بيان ذلك.
دليل عدم توريثهم إذا كان بيت المال منتظماً:
استدل الشافعي رحمه الله تعالى على عدم توريثهم أنه لم يرد لهم نصيب معين من الميراث، في القرآن ولا في السنة، ولو كان لهم حق في التركة لبينه الله عز وجل، ورسوله عليه الصلاة والسلام، كما هو الشأن في أصحاب الفروض، والعصبات.
__________
(1) هديت جملة دعائية. والهداية: الدلالة على الخير.
(2) علانية : جهراً.
(3) شامخة: مرتفعة عالية.
وأيضاً فإن
النبي - صلى الله عليه وسلم - قال: " إن الله عز وجل أعطى كل ذي حق حقه فلا
وصية لوارث" رواه الترمذي (2122) في (الوصايا)، باب ( ما جاء لا وصية لوارث)؛
ورواه النسائي ( 6/247) في (الوصايا)، باب ( إبطال الوصية للوارث)، كلاهما عن عمرو
بن خارجة - رضي الله عنه -، فلو كان لهم شيء من التركة لأعطاهم الله إياه.
لكن المتأخرين من الشافعية رحمهم الله، قد أفتوا بتوريث ذويي الأرحام، وذلك منذ القرن الرابع الهجري، انطلاقاً من أن بيت المال لم يعد منتظماً، ولم يعد يصل لذوي الحقوق منه حقوقهم، فلأن يرجع مال الميت لأرحامه، وغير الوارثين من أقاربه، أولى من أن يذهب إلى غير ذي حق من الأباعد.
أصناف ذوي الأرحام:
يمكن حصر ذوي الأرحام في أربعة أصناف هي:
الأول: من ينتمي إلى الميت، لكون الميت أصلاً له، وهم:
أولاد البنات، مهما نزلوا.
أولاد بنات الابن، وإن نزلوا أيضاً.
الثاني: من ينتمي إليهم الميت لكونهم أصولاً له، وهم:
الأجداد والجدات الرحميون، الذين هم غير من سبق ذكرهم. فالجد الرحمي: هو كل من توسطت بينه وبين الميت أنثى، كالجد أبي الأم، وأبوه، وإن علا.
والجدة الرحمية: هي أيضاً من توسط بينها وبين الميت جد رحمي، كأم أبي الأم، وأمها، وإن علت.
الثالث: من ينتمي إلى أبوي الميت، لكونهما أصلاً جامعاً له وللميت، وهم:
أولاد الأخوات مطلقاً، أي ذكوراً كانوا أم إناثاُ، سواء كانت الأخوات شقيقات أم لأب، أم لأم.
بنات الإخوة الأشقاء، أو لأب، أو لأم.
أولاد الإخوة لأم، ذكوراً كانوا أم إناثاً.
وكل من يدلي إلى الميت بواحد من هؤلاء.
الرابع: من ينتمي إلى أجداد الميت وجداته، لكون هؤلاء الأجداد والجدات أصلاً جامعاً له وللميت، وهم:
الأعمام للأم، والعمات مطلقاً، وبنات الأعمام مطلقاً.
الأخوال والخالات مطلقاً، وإن تباعدوا، وأولادهم وإن تنازلوا.
كيفية توريث ذوي الأرحام:
لكن المتأخرين من الشافعية رحمهم الله، قد أفتوا بتوريث ذويي الأرحام، وذلك منذ القرن الرابع الهجري، انطلاقاً من أن بيت المال لم يعد منتظماً، ولم يعد يصل لذوي الحقوق منه حقوقهم، فلأن يرجع مال الميت لأرحامه، وغير الوارثين من أقاربه، أولى من أن يذهب إلى غير ذي حق من الأباعد.
أصناف ذوي الأرحام:
يمكن حصر ذوي الأرحام في أربعة أصناف هي:
الأول: من ينتمي إلى الميت، لكون الميت أصلاً له، وهم:
أولاد البنات، مهما نزلوا.
أولاد بنات الابن، وإن نزلوا أيضاً.
الثاني: من ينتمي إليهم الميت لكونهم أصولاً له، وهم:
الأجداد والجدات الرحميون، الذين هم غير من سبق ذكرهم. فالجد الرحمي: هو كل من توسطت بينه وبين الميت أنثى، كالجد أبي الأم، وأبوه، وإن علا.
والجدة الرحمية: هي أيضاً من توسط بينها وبين الميت جد رحمي، كأم أبي الأم، وأمها، وإن علت.
الثالث: من ينتمي إلى أبوي الميت، لكونهما أصلاً جامعاً له وللميت، وهم:
أولاد الأخوات مطلقاً، أي ذكوراً كانوا أم إناثاُ، سواء كانت الأخوات شقيقات أم لأب، أم لأم.
بنات الإخوة الأشقاء، أو لأب، أو لأم.
أولاد الإخوة لأم، ذكوراً كانوا أم إناثاً.
وكل من يدلي إلى الميت بواحد من هؤلاء.
الرابع: من ينتمي إلى أجداد الميت وجداته، لكون هؤلاء الأجداد والجدات أصلاً جامعاً له وللميت، وهم:
الأعمام للأم، والعمات مطلقاً، وبنات الأعمام مطلقاً.
الأخوال والخالات مطلقاً، وإن تباعدوا، وأولادهم وإن تنازلوا.
كيفية توريث ذوي الأرحام:
قلنا: عن ذوي
الأرحام يرثون حين لا يوجد من يرث بفرض- غير الزوجين – أو بتعصيب، فإذا لم يوجد
أحد من الورثة، كان الميراث جميعه لذوي الأرحام.
وإن وجد أحد الزوجين، كان ما بقي، بعد فرضه، لهم.
فإن انفرد واحد من ذوي الأرحام، كان المال جميعه له: كمن خلف بنت، استحق كل التركة.وإن اجتمع أكثر من واحد من ذوي الأرحام، كان توريثهم على النحو التالي:
ينزل كل واحد من ذوي الأرحام- ما عدا الأخوال والخالات، والأعمام لأم والعمات- منزلة من يدلي به إلى الميت.
فينزل كل فرع منزلة أصله، وأصله منزلة أصله، وهكذا درجة درجة إلى أن تصل إلى أصل وارث. وكل من نزل منزلة شخص يأخذ ما كان يأخذه ذلك الشخص، فيفرض موت ذلك الشخص، وأن هذا المنزل منزلته وارثه، كابن البنت فإنه ينزل منزلة أمه، وهي البنت، وبنت الأخ تنزل منزلة أبيها، وهو الأخ، وهكذا.
وهذا – كما قلنا- في غير الأخوال والخالات، والأعمام لأم، والعمات.
فالأخوال والخالات ينزلون منزلة الأم، فما يثبت لها، من كل المال عند الانفراد، أو ثلثه، أو سدسه عند عدم الانفراد، يثبت لهم.
أما الأعمام لأم، والعمات، فإنهم ينزلون منزلة الأب، ويرثون ما كان يرثه هو.
2- بعد أن ينزل كل واحد من ذوي الأرحام منزلته – على النحو السابق – يقدم من سبق إلى وارث، سواء قربت رجته إلى الميت، أم بعدت.
فلو اجتمع: بنت بنت البنت، وبنت بنت ابن الابن:
كان المال كله، للثانية، وهي بنت بنت ابن الابن، وإن كانت الأولى، وهي بنت بنت البنت أقرب إلى الميت منها، لأن الثانية سبقت الأولى إلى وارث، إذ الثانية ليس بينها وبين من أدلت به أحد غير وارث.
بينما الأولى بينها وبين من أدلت به من الوارثين شخص غير وارث، وهو بين البنت.
وإن وجد أحد الزوجين، كان ما بقي، بعد فرضه، لهم.
فإن انفرد واحد من ذوي الأرحام، كان المال جميعه له: كمن خلف بنت، استحق كل التركة.وإن اجتمع أكثر من واحد من ذوي الأرحام، كان توريثهم على النحو التالي:
ينزل كل واحد من ذوي الأرحام- ما عدا الأخوال والخالات، والأعمام لأم والعمات- منزلة من يدلي به إلى الميت.
فينزل كل فرع منزلة أصله، وأصله منزلة أصله، وهكذا درجة درجة إلى أن تصل إلى أصل وارث. وكل من نزل منزلة شخص يأخذ ما كان يأخذه ذلك الشخص، فيفرض موت ذلك الشخص، وأن هذا المنزل منزلته وارثه، كابن البنت فإنه ينزل منزلة أمه، وهي البنت، وبنت الأخ تنزل منزلة أبيها، وهو الأخ، وهكذا.
وهذا – كما قلنا- في غير الأخوال والخالات، والأعمام لأم، والعمات.
فالأخوال والخالات ينزلون منزلة الأم، فما يثبت لها، من كل المال عند الانفراد، أو ثلثه، أو سدسه عند عدم الانفراد، يثبت لهم.
أما الأعمام لأم، والعمات، فإنهم ينزلون منزلة الأب، ويرثون ما كان يرثه هو.
2- بعد أن ينزل كل واحد من ذوي الأرحام منزلته – على النحو السابق – يقدم من سبق إلى وارث، سواء قربت رجته إلى الميت، أم بعدت.
فلو اجتمع: بنت بنت البنت، وبنت بنت ابن الابن:
كان المال كله، للثانية، وهي بنت بنت ابن الابن، وإن كانت الأولى، وهي بنت بنت البنت أقرب إلى الميت منها، لأن الثانية سبقت الأولى إلى وارث، إذ الثانية ليس بينها وبين من أدلت به أحد غير وارث.
بينما الأولى بينها وبين من أدلت به من الوارثين شخص غير وارث، وهو بين البنت.
3- إذا استوى
الموجودون من ذوي الأرحام في الإدلاء، فرض أن الميت خلف الوارثين الذين ينتسب
إليهم ذوو الأرحام، وقسم المال – أو الباقي بعد فرض أحد الزوجين – بين هؤلاء
المفروضين، كأنهم موجودون، فمن يحجب منهم لا شيء لمن يدلي به، وما أصاب كل واحد
منهم قسم على من نزل منزلته، كأنه مات وخلفهم وصورة ذلك: أن يموت شخص ويخلف:
7 (عول)
6
6/1 ... أبا أم ... 1
3/1 ... بنتي أختين لأم ... 2
2/1 ... بنت أخت شقيقة ... 3
6/1 ... بنت أخت لأب ... 1
لأبي الأم السدس، لأنه ينزل منزلة الأم التي أدلى بها.
لبنتي الأختين لأم الثلث، لأنهما بمنزلة الأختين لأم اللتين أدلتا بهما.
لبنت الأخت الشقيقة النصف، لأنها بمنزلة الأخت الشقيقة التي أدلت بها.
ولبنت الأخت لأب السدس، لأنها بمنزلة الأخت لأب مع الشقيقة.
ويجب أن يلاحظ هنا أن العول لا يصيب نصيب الزوج، أو الزوجة، فيما لو وجد أحدهما مع ذوي الأرحام، بل يعطي أحد الزوجين نصيبه أولاً، ثم يوزع ما بقي على ذوي الأرحام.
2 ... 4
2/1 ... زوجاً ... 1 ... 2
ع ... وبنتي أختين ... 1 ... 2
فلو ماتت امرأة وخلفت:
لكان للزوج النصف، واحد من اثنين، ويبقى واحد لبنتي الأختين، لكل واحدة نصفه، ولما كان الواحد لا ينقسم عليهما، فسوف نصير إلى تصحيح المسألة، وعندها نأخذ عدد الرؤوس لتباينها مع السهام، ويضرب به أصل المسألة، فما بلغ فمنه تصح: (2×2=4).
فيأخذ الزوج نصيبه مضروباً باثنين(1×2=2)، وتأخذ بنتي الأختين نصيبهما مضروباً(1×2=2) لكل واحد منهما سهم من أربعة أسهم.
ولو كان بدل بنتي الأختين أختان، لكان لهما الثلثان، لعالت المسألة بسهامها على الأختين، وعلى الزوج، ولم يبق للزوج نصف سالم، بل يكون له ثلاثة أسهم من سبعة، بخلاف ما لو كان مع ذوي الأرحام. فإنه يأخذه نصفاً سالماً.
ويستثنى من الضابط السابق – وهو أن ما يصيب كل واحد من المفروضين يقسم على من نزل منزلته كأنه مات وخلفهم،- ما يلي:
7 (عول)
6
6/1 ... أبا أم ... 1
3/1 ... بنتي أختين لأم ... 2
2/1 ... بنت أخت شقيقة ... 3
6/1 ... بنت أخت لأب ... 1
لأبي الأم السدس، لأنه ينزل منزلة الأم التي أدلى بها.
لبنتي الأختين لأم الثلث، لأنهما بمنزلة الأختين لأم اللتين أدلتا بهما.
لبنت الأخت الشقيقة النصف، لأنها بمنزلة الأخت الشقيقة التي أدلت بها.
ولبنت الأخت لأب السدس، لأنها بمنزلة الأخت لأب مع الشقيقة.
ويجب أن يلاحظ هنا أن العول لا يصيب نصيب الزوج، أو الزوجة، فيما لو وجد أحدهما مع ذوي الأرحام، بل يعطي أحد الزوجين نصيبه أولاً، ثم يوزع ما بقي على ذوي الأرحام.
2 ... 4
2/1 ... زوجاً ... 1 ... 2
ع ... وبنتي أختين ... 1 ... 2
فلو ماتت امرأة وخلفت:
لكان للزوج النصف، واحد من اثنين، ويبقى واحد لبنتي الأختين، لكل واحدة نصفه، ولما كان الواحد لا ينقسم عليهما، فسوف نصير إلى تصحيح المسألة، وعندها نأخذ عدد الرؤوس لتباينها مع السهام، ويضرب به أصل المسألة، فما بلغ فمنه تصح: (2×2=4).
فيأخذ الزوج نصيبه مضروباً باثنين(1×2=2)، وتأخذ بنتي الأختين نصيبهما مضروباً(1×2=2) لكل واحد منهما سهم من أربعة أسهم.
ولو كان بدل بنتي الأختين أختان، لكان لهما الثلثان، لعالت المسألة بسهامها على الأختين، وعلى الزوج، ولم يبق للزوج نصف سالم، بل يكون له ثلاثة أسهم من سبعة، بخلاف ما لو كان مع ذوي الأرحام. فإنه يأخذه نصفاً سالماً.
ويستثنى من الضابط السابق – وهو أن ما يصيب كل واحد من المفروضين يقسم على من نزل منزلته كأنه مات وخلفهم،- ما يلي:
أ- أولاد
الإخوة لأم، فيقسم بينهم ما يصيب من يدلون به- وهو الأخ لأم- بالسوية، دون تفريق
بين ذكورهم وإناثهم، كما يرث مورثهم كذلك.
مع أن الأخ لأم، أو الأخت لأم، لو مات أحدها وخلف أولاداً، ذكوراً وإناثاً، قسم ميراثه بينهم، للذكر مثل حظ الأنثيين.
ب- الأخوال والخالات الذين من جهة الأم، يقسم بينهم ما يصيب من ينزلون منزلته – وهو الأم- للذكر مثل حظ الأنثيين.
مع أنه لو مات من ينزلون منزلته- وهو الأم – وخلفتهم كانوا إخوة لأم، وكان الميراث بينهم بالسوية.
قسمة التركة
إن قسمة التركة بين الورثة، هي الثمرة المقصودة بالذات من علم الفرائض، وما تقدم كله وسيلة لها. ولتقسيم التركة عدة طرق، وأبسط هذه الطرق أن تقسم التركة على أصل المسألة، ثم يضرب الناتج بسهام كل وارث. مثال ذلك: مات رجل عن:
24
8/1 ... زوجة ... 3
3/2 ... بنتين ... 16
6/1 ... أم ... 4
ع ... أخ شقيق ... 1
واضح أن المسألة من أربعة وعشرين لتوافق مخرجي الثمن والسدس. فللزوجة الثمن (3)، وللبنتين الثلثان (16) لكل بنت (8)، وللأم السدس (4)، وللأخ الشقيق الباقي تعصيباً، وهو سهم واحد.
فإذا كانت التركة: (4800) ليرة مثلاً، فالعمل أن تقسم التركة على أصل المسألة، ثم نضرب الناتج بنصيب كل وارث:
4800÷24=200 ليرة قيمة السهم الواحد.
فللزوجة إذاً = 200×3=600 ليرة.
للبنين ... = 200×16=3200 ليرة.
للأم = 200×4= 800 ليرة.
للأخ = 200×1= 200 ليرة.ويكون المجموع 4800 ليرة، وهو قيمة التركة.
وهناك طريقة أخرى، وهي:
أن نضرب نصيب كل وارث بالتركة، ثم نقسم الحاصل على أصل المسألةز
مثال ذلك: مات رجل عن:
12
3/1 ... أم ... 4
4/1 ... زوجة ... 3
ع ... عم ... 5
...
المسألة من (12) لتباين مخرجي فرض الأم والزوجة، للأم أربعة، وهي الثلث، وللزوجة الربع ثلاثة، والباقي تعصيباً، وهو خمسة.
فلو فرضنا أن التركة كانت (100) دينار،
فيكون نصيب الأم : ... = 3/1 33.
مع أن الأخ لأم، أو الأخت لأم، لو مات أحدها وخلف أولاداً، ذكوراً وإناثاً، قسم ميراثه بينهم، للذكر مثل حظ الأنثيين.
ب- الأخوال والخالات الذين من جهة الأم، يقسم بينهم ما يصيب من ينزلون منزلته – وهو الأم- للذكر مثل حظ الأنثيين.
مع أنه لو مات من ينزلون منزلته- وهو الأم – وخلفتهم كانوا إخوة لأم، وكان الميراث بينهم بالسوية.
قسمة التركة
إن قسمة التركة بين الورثة، هي الثمرة المقصودة بالذات من علم الفرائض، وما تقدم كله وسيلة لها. ولتقسيم التركة عدة طرق، وأبسط هذه الطرق أن تقسم التركة على أصل المسألة، ثم يضرب الناتج بسهام كل وارث. مثال ذلك: مات رجل عن:
24
8/1 ... زوجة ... 3
3/2 ... بنتين ... 16
6/1 ... أم ... 4
ع ... أخ شقيق ... 1
واضح أن المسألة من أربعة وعشرين لتوافق مخرجي الثمن والسدس. فللزوجة الثمن (3)، وللبنتين الثلثان (16) لكل بنت (8)، وللأم السدس (4)، وللأخ الشقيق الباقي تعصيباً، وهو سهم واحد.
فإذا كانت التركة: (4800) ليرة مثلاً، فالعمل أن تقسم التركة على أصل المسألة، ثم نضرب الناتج بنصيب كل وارث:
4800÷24=200 ليرة قيمة السهم الواحد.
فللزوجة إذاً = 200×3=600 ليرة.
للبنين ... = 200×16=3200 ليرة.
للأم = 200×4= 800 ليرة.
للأخ = 200×1= 200 ليرة.ويكون المجموع 4800 ليرة، وهو قيمة التركة.
وهناك طريقة أخرى، وهي:
أن نضرب نصيب كل وارث بالتركة، ثم نقسم الحاصل على أصل المسألةز
مثال ذلك: مات رجل عن:
12
3/1 ... أم ... 4
4/1 ... زوجة ... 3
ع ... عم ... 5
...
المسألة من (12) لتباين مخرجي فرض الأم والزوجة، للأم أربعة، وهي الثلث، وللزوجة الربع ثلاثة، والباقي تعصيباً، وهو خمسة.
فلو فرضنا أن التركة كانت (100) دينار،
فيكون نصيب الأم : ... = 3/1 33.
فيكون نصيب
الزوجة: ... =25.
ويكون نصيب العم: = 3/2 41.
مثال آخر: ماتت امرأة عن:
4
4/1 ... زوج ... 1
ع ... أخت شقيقة ... 1
2/1 ... بنت ابن ... 2
للزوج الربع (1)، وللبنت النصف (2)، وللأخت الشقيقة الباقي تعصيباً، وهو (1)، لأنها عصبة مع الغير.
وأصل المسألة من أربعة، لتداخل مخرج فرض البنت بمخرج فرض الزوج. فلو فرضنا أن التركة كانت (44) ألف ليرة:
لكان نصيب الزوج: = 11 ألف ليرة.
نصيب الشقيقة : = 11 ألف ليرة.
نصيب البنت : = 22 ألف ليرة
المسائل المشهورة في المواريث
لقد اشتهر في المواريث مسائل أخذت ألقاباً معينة، عرفت بها بين علماء الفرائض:
إما لحدوث خلاف فيها، وإما نسبة إلى من سئل عنها، أو قضى فيها.
ولقد مر بعضها أثناء أبحاثنا، في قواعد هذا العلم، وفي ثنايا أحكامه.
وها نحن نذكر تحت هذا العنوان أشهر هذه المسائل، ليعرفها من يدرس هذا الكتاب، ويطلع عليها من لم يتح له أن يرجع إلى المطولات من أمهات كتب هذا الفن العظيم.
1- المشركة.
وتسمى أيضاً المشتركة، والحمارية.
وقد مرت معنا في بحث الإخوة، وهي كما تعلم
6
18
2/1
زوج
3
9
6/1
أم
1
3
3/1
أخوان لأم فأكثر
2
4
أخ شقيق، فأكثر
2
وعرفت أن عمر بن الخطاب - رضي الله عنه - قضى فيها أولاً، فأسقط الإخوة الأشقاء، لكونهم عصبة، ولم يبق لهم شيء بعد الفروض.
ثم عاد ثانياُ وقضى بالتشريك بين الأشقاء والأخوة لأم، فألغى الأب، وجعلهم جميعاً إخوة لأم.
2- العمريتان.
سمينا بذلك لقضاء عمر - رضي الله عنه - فيهما، كما مر معنا، وعرفت أنه أعطى الأم فيهما ثلث الباقي بعد فرض أحد الزوجين. وهما
6
2/1 ... زوج ... 3
3/1 با ... أم ... 1
ع ... أب ... 2
12
4/1 ... زوجة ... 3
3/1 با ... أم ... 3
ع ... أب ... 6
3- المباهلة. وهي:
8 ( عول )
6
2/1 ... زوج ... 3
3/1 ... أم ... 2
2/1 ... أخت شقيقة ... 3
ويكون نصيب العم: = 3/2 41.
مثال آخر: ماتت امرأة عن:
4
4/1 ... زوج ... 1
ع ... أخت شقيقة ... 1
2/1 ... بنت ابن ... 2
للزوج الربع (1)، وللبنت النصف (2)، وللأخت الشقيقة الباقي تعصيباً، وهو (1)، لأنها عصبة مع الغير.
وأصل المسألة من أربعة، لتداخل مخرج فرض البنت بمخرج فرض الزوج. فلو فرضنا أن التركة كانت (44) ألف ليرة:
لكان نصيب الزوج: = 11 ألف ليرة.
نصيب الشقيقة : = 11 ألف ليرة.
نصيب البنت : = 22 ألف ليرة
المسائل المشهورة في المواريث
لقد اشتهر في المواريث مسائل أخذت ألقاباً معينة، عرفت بها بين علماء الفرائض:
إما لحدوث خلاف فيها، وإما نسبة إلى من سئل عنها، أو قضى فيها.
ولقد مر بعضها أثناء أبحاثنا، في قواعد هذا العلم، وفي ثنايا أحكامه.
وها نحن نذكر تحت هذا العنوان أشهر هذه المسائل، ليعرفها من يدرس هذا الكتاب، ويطلع عليها من لم يتح له أن يرجع إلى المطولات من أمهات كتب هذا الفن العظيم.
1- المشركة.
وتسمى أيضاً المشتركة، والحمارية.
وقد مرت معنا في بحث الإخوة، وهي كما تعلم
6
18
2/1
زوج
3
9
6/1
أم
1
3
3/1
أخوان لأم فأكثر
2
4
أخ شقيق، فأكثر
2
وعرفت أن عمر بن الخطاب - رضي الله عنه - قضى فيها أولاً، فأسقط الإخوة الأشقاء، لكونهم عصبة، ولم يبق لهم شيء بعد الفروض.
ثم عاد ثانياُ وقضى بالتشريك بين الأشقاء والأخوة لأم، فألغى الأب، وجعلهم جميعاً إخوة لأم.
2- العمريتان.
سمينا بذلك لقضاء عمر - رضي الله عنه - فيهما، كما مر معنا، وعرفت أنه أعطى الأم فيهما ثلث الباقي بعد فرض أحد الزوجين. وهما
6
2/1 ... زوج ... 3
3/1 با ... أم ... 1
ع ... أب ... 2
12
4/1 ... زوجة ... 3
3/1 با ... أم ... 3
ع ... أب ... 6
3- المباهلة. وهي:
8 ( عول )
6
2/1 ... زوج ... 3
3/1 ... أم ... 2
2/1 ... أخت شقيقة ... 3
للزوج النصف
(3) وللأم الثلث (2)، وللأخت الشقيقة النصف (3). وأصل المسألة من (6) وقد عالت إلى
(8). وهي أول مسألة عالت في الإسلام.
وقد مرت معنا أيضاً، من غير أن نطلق عليها هذا اللقب في حينها.
وقد وقعت هذه المسألة في صدر خلافة عمر - رضي الله عنه -، فاستشار الصحابة فيها فأشار العباس - رضي الله عنه -، أن يقسم عليهم بقدر سهامهم، فصاروا إلى ذلك.
وفي رواية أن عمر قال لهؤلاء الورثة: ( لا أجد فرضاً في كتاب الله، ولا أدري من قدمه الله تعالى، فأقدمه، ولا من أخره فأؤخره، ولكن رأيت رأياً، فإن كان صواباً فمن الله، وإن كان خطأ فمني، أرى أن أدخل النقص على الكل)، فقسم بالعول، ولم يخالفه أحد، على أن ولي الخلافة عثمان - رضي الله عنه -. فأظهر عبدالله بن عباس رضي الله عنهما مخالفته لما فعل عمر، وقال: لو قدموا من قدمه الله، وأخروا من أخره الله، ما عالت فريضة قط، فقيل له: من قدمه الله، ومن أخره؟ قال: الزوج والزوجة والأم والجدة ممن قدمه الله، أما من أخره الله، فالبنات، وبنات الابن، والأخوات لأب وأم، والأخوات لأب، فتارة يفرض لهن، وتارة يكن عصبة، ويدخل النقص على هؤلاء الأربع.
فلما ناقشوه في هذا الرأي، قال من شاء باهلته، إن الذي أحصى رمل عالج لم يجعل في المال نصفاً، ونصفاً، وثلثا، فقيل له: هلا ذكرت ذلك في زمن عمر؟ فقال: كان مهيباً فهبته.
[ عالج: موضع في البادية كثير الرمل. وقوله باهلته: هو من قول الله تعالى: { فَمَنْ حَآجَّكَ فِيهِ مِن بَعْدِ مَا جَاءكَ مِنَ الْعِلْمِ فَقُلْ تَعَالَوْاْ نَدْعُ أَبْنَاءنَا وَأَبْنَاءكُمْ وَنِسَاءنَا وَنِسَاءكُمْ وَأَنفُسَنَا وأَنفُسَكُمْ ثُمَّ نَبْتَهِلْ فَنَجْعَل لَّعْنَةَ اللّهِ عَلَى الْكَاذِبِينَ } [ آل عمران : 61].
ومن هنا سميت هذه المسألة بالمباهلة.
4- المنبرية.
27 (عول )
24
8/1 ... زوجة ... 3
6/1 ... أب ... 4
6/1 ... أم ... 4
3/2 ... بنتان ... 16
وهي:
وقد مرت معنا أيضاً، من غير أن نطلق عليها هذا اللقب في حينها.
وقد وقعت هذه المسألة في صدر خلافة عمر - رضي الله عنه -، فاستشار الصحابة فيها فأشار العباس - رضي الله عنه -، أن يقسم عليهم بقدر سهامهم، فصاروا إلى ذلك.
وفي رواية أن عمر قال لهؤلاء الورثة: ( لا أجد فرضاً في كتاب الله، ولا أدري من قدمه الله تعالى، فأقدمه، ولا من أخره فأؤخره، ولكن رأيت رأياً، فإن كان صواباً فمن الله، وإن كان خطأ فمني، أرى أن أدخل النقص على الكل)، فقسم بالعول، ولم يخالفه أحد، على أن ولي الخلافة عثمان - رضي الله عنه -. فأظهر عبدالله بن عباس رضي الله عنهما مخالفته لما فعل عمر، وقال: لو قدموا من قدمه الله، وأخروا من أخره الله، ما عالت فريضة قط، فقيل له: من قدمه الله، ومن أخره؟ قال: الزوج والزوجة والأم والجدة ممن قدمه الله، أما من أخره الله، فالبنات، وبنات الابن، والأخوات لأب وأم، والأخوات لأب، فتارة يفرض لهن، وتارة يكن عصبة، ويدخل النقص على هؤلاء الأربع.
فلما ناقشوه في هذا الرأي، قال من شاء باهلته، إن الذي أحصى رمل عالج لم يجعل في المال نصفاً، ونصفاً، وثلثا، فقيل له: هلا ذكرت ذلك في زمن عمر؟ فقال: كان مهيباً فهبته.
[ عالج: موضع في البادية كثير الرمل. وقوله باهلته: هو من قول الله تعالى: { فَمَنْ حَآجَّكَ فِيهِ مِن بَعْدِ مَا جَاءكَ مِنَ الْعِلْمِ فَقُلْ تَعَالَوْاْ نَدْعُ أَبْنَاءنَا وَأَبْنَاءكُمْ وَنِسَاءنَا وَنِسَاءكُمْ وَأَنفُسَنَا وأَنفُسَكُمْ ثُمَّ نَبْتَهِلْ فَنَجْعَل لَّعْنَةَ اللّهِ عَلَى الْكَاذِبِينَ } [ آل عمران : 61].
ومن هنا سميت هذه المسألة بالمباهلة.
4- المنبرية.
27 (عول )
24
8/1 ... زوجة ... 3
6/1 ... أب ... 4
6/1 ... أم ... 4
3/2 ... بنتان ... 16
وهي:
المسألة من
(24) لوجود التوافق بين مخرجي الثمن والسدس، وقد عالت إلى (27).
للزوجة الثمن (3)، وللأب السدس(4)، وللأم السدس (4)، وللبنتين الثلثان (16).
وسميت هذه المسألة بالمنبرية، لأن علياً - رضي الله عنه - كان يخطب على المنبر، وكان قد بدأ خطابه بقوله: الحمد لله الذي يجزي كل نفس بما تسعى، ثم سئل عن هذه المسألة، فأجاب على الفور؛ والمرأة قد صار ثمنها تسعاً، ثم استمر في خطبته،فكان ذلك من نباهته، وحضور بديهته.
3 ... 9
3/1 ... أم ... 1 ... 3
ع ... جد ... 2 ... 4
أخت شقيقة ... 2
5- الخرقاء.
وهي:
للأم الثلث، والباقي للجد والأخت مقاسمة للذكر مثل حظ الأنثيين.
المسألة من ثلاثة، وتصح من تسعة، للأم (3)، وللجد (4)، وللأخت(2).
وسميت هذه المسألة الخرقاء، كأن أقوال الصحابة خرقتها، أو أنها خرقت اتفاقهم، فقد اختلفوا فيها على سبعة أقوال، وما ذكرناه هو مذهبنا.
6- الأكدرية.
9 (عول)
6 ... 27
2/1 ... زوج ... 3 ... 9
3/1 ... أم ... 2 ... 6
6/1 ... جد ... 1 ... 8
2/1 ... أخت شقيقة، أو لأب ... 3 ... 4
وقد مرت معنا وهي:
للزوج النصف عائلاً، وللأم الثلث عائلاً، وللجد السدس عائلاً، وللأخت النصف عائلاً. فالمسألة من ستة، وتعول إلى تسعة. ثم بعد هذا يعود الجد إلى الأخت فيقاسمها الفريضة، ويأخذ معها للذكر مثل حظ الأنثيين، ولما كان نصيبه، وهو (1) من تسعة، ونصيبها (3) من تسعة لا ينقسمان عليهما للذكر مثل حظ الأنثيين أخذنا عدد الرؤوس، لتباينها مع السهام، وضربنا بها أصل المسألة، فكان تصحيح المسألة من (27)، للزوج (9)، وللأم (6)، وللجد (8)، وللأخت (4). وسميت هذه المسألة بالأكدرية، لأنها كدرت على زيد بن ثابت مذهبه من ثلاثة أوجه، أعال بالجد، وفرض للأخت، وجمع سهام الفرض وقسمها على التعصيب.
وإنما فرض للأخت، ولما يجعلها عصبة، لأنه لم يبق لها شيء، ولا وجه إلى القسمة، لأنه ينقص نصيب الجد عن السدس.
7- اليتيمتان.
للزوجة الثمن (3)، وللأب السدس(4)، وللأم السدس (4)، وللبنتين الثلثان (16).
وسميت هذه المسألة بالمنبرية، لأن علياً - رضي الله عنه - كان يخطب على المنبر، وكان قد بدأ خطابه بقوله: الحمد لله الذي يجزي كل نفس بما تسعى، ثم سئل عن هذه المسألة، فأجاب على الفور؛ والمرأة قد صار ثمنها تسعاً، ثم استمر في خطبته،فكان ذلك من نباهته، وحضور بديهته.
3 ... 9
3/1 ... أم ... 1 ... 3
ع ... جد ... 2 ... 4
أخت شقيقة ... 2
5- الخرقاء.
وهي:
للأم الثلث، والباقي للجد والأخت مقاسمة للذكر مثل حظ الأنثيين.
المسألة من ثلاثة، وتصح من تسعة، للأم (3)، وللجد (4)، وللأخت(2).
وسميت هذه المسألة الخرقاء، كأن أقوال الصحابة خرقتها، أو أنها خرقت اتفاقهم، فقد اختلفوا فيها على سبعة أقوال، وما ذكرناه هو مذهبنا.
6- الأكدرية.
9 (عول)
6 ... 27
2/1 ... زوج ... 3 ... 9
3/1 ... أم ... 2 ... 6
6/1 ... جد ... 1 ... 8
2/1 ... أخت شقيقة، أو لأب ... 3 ... 4
وقد مرت معنا وهي:
للزوج النصف عائلاً، وللأم الثلث عائلاً، وللجد السدس عائلاً، وللأخت النصف عائلاً. فالمسألة من ستة، وتعول إلى تسعة. ثم بعد هذا يعود الجد إلى الأخت فيقاسمها الفريضة، ويأخذ معها للذكر مثل حظ الأنثيين، ولما كان نصيبه، وهو (1) من تسعة، ونصيبها (3) من تسعة لا ينقسمان عليهما للذكر مثل حظ الأنثيين أخذنا عدد الرؤوس، لتباينها مع السهام، وضربنا بها أصل المسألة، فكان تصحيح المسألة من (27)، للزوج (9)، وللأم (6)، وللجد (8)، وللأخت (4). وسميت هذه المسألة بالأكدرية، لأنها كدرت على زيد بن ثابت مذهبه من ثلاثة أوجه، أعال بالجد، وفرض للأخت، وجمع سهام الفرض وقسمها على التعصيب.
وإنما فرض للأخت، ولما يجعلها عصبة، لأنه لم يبق لها شيء، ولا وجه إلى القسمة، لأنه ينقص نصيب الجد عن السدس.
7- اليتيمتان.
وهما مسألتان:
... الأولى: ... ... ... ... ... ... الثانية
2
2/1 ... زوج ... 1
2/1 ... أخت لأب ... 1
2
2/1 ... زوج ... 1
2/1 ... أخت شقيقة ... 1
ففي هاتين المسألتين يأخذ الزوج النصف، والأخت النصف، وليس في الفرائض كلها مسألة يورث فيها المال بفريضتين، متساويتين، إلا في هاتين المسألتين، ولذلك سميتا اليتيمتين.
8- أم الفروخ. وهي:
10 (عول)
6
2/1 ... زوج ... 3
6/1 ... أم ... 1
3/1 ... أختان لأم ... 2
3/2 ... أختان لأبوين ... 4
للزوج النصف، وللأم السدس، وللأختين للأم الثلث، وللأختين للأبوين الثلثان.
أصل المسألة (6)، وتعول إلى (10).
وسميت هذه المسألة بأم الفروخ، لأنها أكثر المسائل عولاً، فشبهت الأربعة الزوائد بالفروخ، وتسمى أيضاً الشريحية، لأن القاضي شريحاً أول من قضى فيها.
9- أم الأرامل.
وهي:
17 (عول)
12
4/1 ... ثلاث زوجات ... 3
6/1 ... جدتان ... 2
3/1 ... أربع أخوات لأم ... 4
3/2 ... ثمان أخوات شقيقات ... 8
للزوجات الربع(3)، لكل زوجة سهم، وللجدتين السدس (2)، لكل جدة (1)، وللأخوات لأم الثلث (4)، لكل أخت (1)، وللأخوات الشقيقات الثلثان (8)، لكل أخت (1). أصل المسألة (12) وتعول إلى (17) سميت أم الأرامل، لأن الورثة فيها كلهن إناث. وفي هذه المسألة يلغز، أيضاً، فيقال: رجل مات وترك سبعة عشر ديناراً، وسبع عشرة امرأة، أصاب كل امرأة دينار واحد.
10- المروانية.
وهي:
9 (عول)
6
2/1 ... زوج ... 3
3/2 ... أختان شقيقتان ... 4
م ... أختان لأب
3/1 ... أختان لأم ... 2
للزوج النصف عائلاً (3)، وللأختين لأبوين الثلثان عائلاً (4)، والأختان لأب محجوبتان بالأختين الشقيقتين، لاستغراقهما الثلثين. وللأختين لأم الثلث عائلاً (2).
أصل المسألة من (6) وتعول إلى (9).
سميت مروانية، لوقوعها في زمن مروان بن الحكم.
وتسمى الغراء، لاشتهارها بين العلماء.
11- الحمزية:
وهي
6
72
6/1
ثلاث جدات متحاذيات
1
12
ع
جد
5
30
أخت شقيقة
2
2/1 ... زوج ... 1
2/1 ... أخت لأب ... 1
2
2/1 ... زوج ... 1
2/1 ... أخت شقيقة ... 1
ففي هاتين المسألتين يأخذ الزوج النصف، والأخت النصف، وليس في الفرائض كلها مسألة يورث فيها المال بفريضتين، متساويتين، إلا في هاتين المسألتين، ولذلك سميتا اليتيمتين.
8- أم الفروخ. وهي:
10 (عول)
6
2/1 ... زوج ... 3
6/1 ... أم ... 1
3/1 ... أختان لأم ... 2
3/2 ... أختان لأبوين ... 4
للزوج النصف، وللأم السدس، وللأختين للأم الثلث، وللأختين للأبوين الثلثان.
أصل المسألة (6)، وتعول إلى (10).
وسميت هذه المسألة بأم الفروخ، لأنها أكثر المسائل عولاً، فشبهت الأربعة الزوائد بالفروخ، وتسمى أيضاً الشريحية، لأن القاضي شريحاً أول من قضى فيها.
9- أم الأرامل.
وهي:
17 (عول)
12
4/1 ... ثلاث زوجات ... 3
6/1 ... جدتان ... 2
3/1 ... أربع أخوات لأم ... 4
3/2 ... ثمان أخوات شقيقات ... 8
للزوجات الربع(3)، لكل زوجة سهم، وللجدتين السدس (2)، لكل جدة (1)، وللأخوات لأم الثلث (4)، لكل أخت (1)، وللأخوات الشقيقات الثلثان (8)، لكل أخت (1). أصل المسألة (12) وتعول إلى (17) سميت أم الأرامل، لأن الورثة فيها كلهن إناث. وفي هذه المسألة يلغز، أيضاً، فيقال: رجل مات وترك سبعة عشر ديناراً، وسبع عشرة امرأة، أصاب كل امرأة دينار واحد.
10- المروانية.
وهي:
9 (عول)
6
2/1 ... زوج ... 3
3/2 ... أختان شقيقتان ... 4
م ... أختان لأب
3/1 ... أختان لأم ... 2
للزوج النصف عائلاً (3)، وللأختين لأبوين الثلثان عائلاً (4)، والأختان لأب محجوبتان بالأختين الشقيقتين، لاستغراقهما الثلثين. وللأختين لأم الثلث عائلاً (2).
أصل المسألة من (6) وتعول إلى (9).
سميت مروانية، لوقوعها في زمن مروان بن الحكم.
وتسمى الغراء، لاشتهارها بين العلماء.
11- الحمزية:
وهي
6
72
6/1
ثلاث جدات متحاذيات
1
12
ع
جد
5
30
أخت شقيقة
30
أخت لأب
0
م
أخت لأم
0
هذه المسألة على مذهب الشافعي من مسائل المعادة، فإن الشقيقة، تعد الأخت لأب على الجد، ثم تأخذ نصيبها.
هذه المسألة من (6)، للجدات السدس (1)، وللجد والأختين الباقي (5)، والأخت لأم محجوبة بالجد.
ونصيب الجدات، لا ينقسم عليهن، وبين عدد رؤوسهن وسهامهن تباين، فنحفظ عدد الرؤوس.
ونصيب الجد والأختين (5) وعدد رؤوسهن أربعة، باعتبار الجد يعد كأختين، فبين الرؤوس وبين السهام أيضاً تباين، فنحفظ عدد الرؤوس، ثم ننظر بين عدد رؤوس الجدات (3) وبين عدد رؤوس الجد والأختين (4) فنجد أنهما متباينان، فنضرب عدد الرؤوس ببعضهما (3×4=12)، ونضرب بالحاصل أصل المسألة (6×12=72). للجدات (1×12=12)، لكل جدة (4) أسهم، للجد والأختين (5×12=60)، للجد نصفها (30)، وللأخت الشقيقة نصفها (30) أيضاً، وهو نصيبها ونصيب الأخت لأب.
وسميت هذه المسألة بهذا الاسم، لأن حمزة الزيات سئل عنها فأجاب بهذا الجواب.
12- الدينارية:
وهي:
24
600
8/1
زوجة
3
75
6/1
جدة
4
100
3/2
بنتان
16
400
ع
اثنا عشر أخأ لأب
1
24
أخت لأب
1
والتركة في هذه المسألة كانت (600) دينار. المسألة من أربعة وعشرين، وتصح، من ستمائة، لأن بين نصيب الأخوة والأخت، وعدد رؤوسهن تبايناً: فنضرب أصل المسألة، بعدد الرؤوس (24×25=600) فيخرج تصحيح المسألة. للزوجة الثمن (75) ديناراً، وللجدة السدس (100) دينار، وللبنتين الثلثان (400) دينار، وللأخوة لأب والأخت لأب الباقي (25) ديناراً، لكل اخ ديناران، وللأخت دينار واحد.
ولهذا سميت هذه المسألة بالدينارية، وفيها يلغز، فيقال: رجل خلف ستمائة دينار، وسبعة عشر وارثاً ذكوراً وإناثاً، فأصاب أحدهم دينار واحد.
13- الامتحان.
أصل
24 ... تصحيح
30240
8/1 ... 4 زوجات ... 3 ... 3780
6/1 ... 5 جدات ... 4 ... 5040
3/2 ... 7بنات ... 16 ... 20160
ع ... 9 أخوات لأب ... 1 ... 1260
وهي:
أخت لأب
0
م
أخت لأم
0
هذه المسألة على مذهب الشافعي من مسائل المعادة، فإن الشقيقة، تعد الأخت لأب على الجد، ثم تأخذ نصيبها.
هذه المسألة من (6)، للجدات السدس (1)، وللجد والأختين الباقي (5)، والأخت لأم محجوبة بالجد.
ونصيب الجدات، لا ينقسم عليهن، وبين عدد رؤوسهن وسهامهن تباين، فنحفظ عدد الرؤوس.
ونصيب الجد والأختين (5) وعدد رؤوسهن أربعة، باعتبار الجد يعد كأختين، فبين الرؤوس وبين السهام أيضاً تباين، فنحفظ عدد الرؤوس، ثم ننظر بين عدد رؤوس الجدات (3) وبين عدد رؤوس الجد والأختين (4) فنجد أنهما متباينان، فنضرب عدد الرؤوس ببعضهما (3×4=12)، ونضرب بالحاصل أصل المسألة (6×12=72). للجدات (1×12=12)، لكل جدة (4) أسهم، للجد والأختين (5×12=60)، للجد نصفها (30)، وللأخت الشقيقة نصفها (30) أيضاً، وهو نصيبها ونصيب الأخت لأب.
وسميت هذه المسألة بهذا الاسم، لأن حمزة الزيات سئل عنها فأجاب بهذا الجواب.
12- الدينارية:
وهي:
24
600
8/1
زوجة
3
75
6/1
جدة
4
100
3/2
بنتان
16
400
ع
اثنا عشر أخأ لأب
1
24
أخت لأب
1
والتركة في هذه المسألة كانت (600) دينار. المسألة من أربعة وعشرين، وتصح، من ستمائة، لأن بين نصيب الأخوة والأخت، وعدد رؤوسهن تبايناً: فنضرب أصل المسألة، بعدد الرؤوس (24×25=600) فيخرج تصحيح المسألة. للزوجة الثمن (75) ديناراً، وللجدة السدس (100) دينار، وللبنتين الثلثان (400) دينار، وللأخوة لأب والأخت لأب الباقي (25) ديناراً، لكل اخ ديناران، وللأخت دينار واحد.
ولهذا سميت هذه المسألة بالدينارية، وفيها يلغز، فيقال: رجل خلف ستمائة دينار، وسبعة عشر وارثاً ذكوراً وإناثاً، فأصاب أحدهم دينار واحد.
13- الامتحان.
أصل
24 ... تصحيح
30240
8/1 ... 4 زوجات ... 3 ... 3780
6/1 ... 5 جدات ... 4 ... 5040
3/2 ... 7بنات ... 16 ... 20160
ع ... 9 أخوات لأب ... 1 ... 1260
وهي:
الزوجات : (3 × 1260) = (03780)
الجدات : (4 × 1260) = (05040)
البنات : (16 × 1260) = (20160)
الأخوات : (1 × 1260) = (01260)
... ... ... ... ( 30240)
وفي هذه المسألة يلغز ويمتحن، فيقال: رجل خلف أصنافاً عدد كل صنف أقل من عشرة، ولا تصح المسألة إلا مما يزيد على ثلاثين ألفاً.
مسائل محلولة في شتى أبواب الفرائض
لقد سردنا معظم أحكام الفرائض قبل أبحاث الحساب، عارية عن رسم مسائل حسابية، اصطلح علماء الفرائض أن يرسموها في كل باب من أبواب المواريث، تقريراً لأحكامه، وتبياناً لطرقه في توزيع الشركة على أصحابها.
والذي حملنا على تأخير ذكر تلك المسائل، إلى ما بعد أبحاث الحساب، إنما هو خوفنا أن يكون عملنا مبيناً على قواعد مجهولة غالباً للدارسين لهذا الفن، قبل أن يصلوا إلى قواعد الحساب، وحل المسائل.
أما الآن، وبعد دراستنا لمسائل الحساب، يبدو ذكرنا لتلك المسائل أمراً معقولاً ومقبولاً، بل هو لازم وضروري.
وها نحن نذكر- إضافة لما مر معنا – نماذج من المسائل المحلولة، والمشروحة في شتى أبواب المواريث، زيادة في الإيضاح، وتقريباً لقواعد هذا العلم، وأحكامه ومسائله، إلى أذهان الراغبين في معرفته، والمحبين لدراسته، سائلين المولى عز وجل النفع لنا ولهم، والهداية إلى سواء السبيل، وهو حسبنا ونعم الوكيل.
الكلمات المفتاحية :
الفقه الشافعي
هذه التدوينة قابلة للنسخ اذا اعجبتك قم بنسخ الرابط من هذه الروابط الثلاثة والصقه بموقعك
URL: HTML link code: BB (forum) link code:


ليست هناك تعليقات: